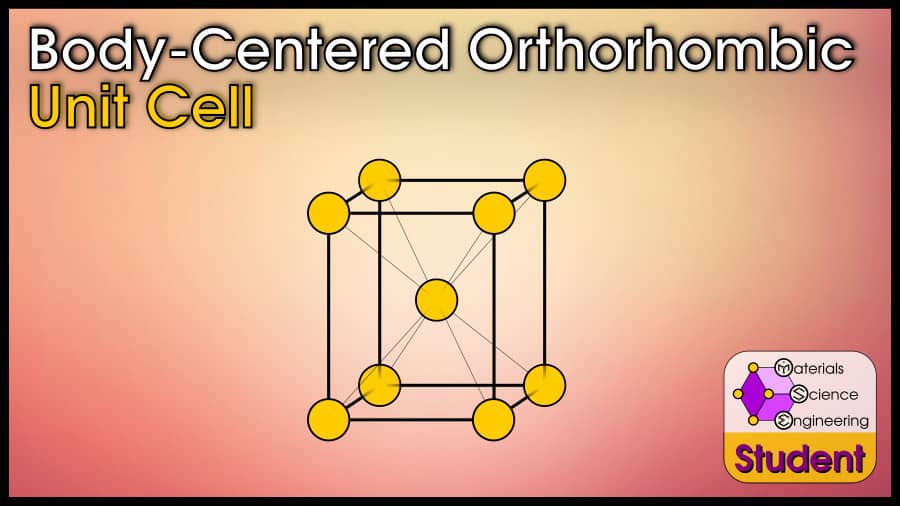
Body-Centered Orthorhombic Unit Cell – Materials Science & Engineering

The body-centered orthorhombic unit cell looks like a box with 3 different edge lengths, with an atom on each corner and another in the center.

Since body-centered orthorhombic is one of the less-common crystal structures, I’m assuming someone searching for this is a somewhat advanced student in materials science, so I’ll give you the facts quickly and with little explanation. If you are new to materials science and don’t know what something means, you can check out my articles on the FCC, BCC, or HCP crystals, which explain terminology more slowly.

As far as I know, there are no real-world materials that exhibit a body-centered orthorhombic unit cell. If this structure were to exist, it would be a box with 3 different side lengths, with an atom on each corner and in the center. There are “body-centered orthorhombic” crystals based on the Bravais lattice, which exist with multiple atoms that overall displays primitive orthorhombic symmetry. The body-centered orthorhombic unit cell would belong to space group #71 or Immm, with Pearson symbol oI2. There is no prototype or Strukturbericht for body-centered orthorhombic, since it does not exist with real atoms.

The body-centered orthorhombic unit cell can be imagined as a box with 3 different side lengths, with an atom on each corner and in the very center. Pure materials never take this crystal structure, and it exists only mathematically. Body-centered orthorhombic has 2 atoms per unit cell, lattice constants a, b, and c, all angles α=90º, Coordination Number CN=8, and Atomic Packing Factor $APF=\frac{8 \pi r^3}{3abc}$ .

Outline

Common Examples of Body-Centered Orthorhombic Materials
Body-Centered Orthorhombic Coordination Number
Body-Centered Orthorhombic Lattice Constants
Body-Centered Orthorhombic Atomic Packing Factor
Final Thoughts
References and Further Reading

Common Examples of Body-Centered Orthorhombic Materials

None.

However, there are still materials made of multiple kinds of atoms that have a body-centered orthorhombic Bravais lattice, such as high pressure GaAs, MoPt₂, and SiS₂.

Body-Centered Orthorhombic Coordination Number

You can think of orthorhombic as a distortion of the simple cubic crystal. However, with the atom in the center, it maintains it’s 8-fold coordination number regardless of each edge length.

Body-centered orthorhombic has 8 nearest neighbors, but remember there are no real materials that take this crystal structure.

Body-Centered Orthorhombic Lattice Constants

The orthorhombic shape is like a cube, where all sides are at 90º to each other, but with edge lengths distorted so there are three different edge lengths. Thus, the body-centered orthorhombic crystal has 3 lattice parameters: a, b, and c, which have an angle of 90º to each other.

If we try to stay within the hard sphere model, we see that the close packed direction would be along one body diagonal. If the atoms touched in that direction, half of the body diagonal length would be $2r$ , and the lattice parameter lengths would need to fit the 3D distance formula $4r=\sqrt{a^2+b^2+c^2}$ .

By definition, body-centered orthorhombic has 3 lattice constants of different lengths: a, b, and c; each at 90º to each other.

If you wanted to describe the simple orthorhombic crystal with math, you would describe the cell with the vectors:

$\vec{a_1}=a\hat{x}$
$\vec{a_2}=b\hat{y}$
$\vec{a_2}=\frac{a}{2}\hat{x}+\frac{b}{2}\hat{y}+\frac{c}{2}\hat{z}$

Body-Centered Orthorhombic Atomic Packing Factor

There is no simple answer for the body-centered orthorhombic APF, because the answer changes depending on the side lengths.

The volume of an orthorhombic unit cell is $abc$ , obtained by multiplying the lattice parameters times each other.

There is 1 atom split between each of the 8 corners of the cell, and 1 more atom in the center, so the total is two full atoms with a spherical radius of $\frac{4}{3} \pi r^3$ .

This allows us to write the theoretical APF in terms of the atomic radius and lattice constants:

$APF=\frac{2\cdot\frac{4}{3} \pi r^3}{abc}=\frac{8 \pi r^3}{3abc}$

If we further assumed that the body-centered diagonal is completely close-packed, then the theoretical APF can be written as

$APF=\frac{8 \pi r^3}{3abc}=\frac{8 \pi (\frac{\sqrt{a^2+b^2+c^2}}{4})^3}{3abc}=\frac{8 \pi (\sqrt{a^2+b^2+c^2})^3}{192abc}$

where $r=\frac{\sqrt{a^2+b^2+c^2}}{4}$

Final Thoughts

The body-centered orthorhombic crystal system does NOT exist in real life, and only arises by mathematical definition. There are several crystals which have a body-centered orthorhombic Bravais lattice, but these crystals have a more complicated “basis” which leads to its characteristic asymmetrical lattice parameters.

References and Further Reading

If you want to know more about the basics of crystallography, check out this article.

If you weren’t sure about the difference between crystal structure and Bravais lattice, check out this article.

I also mentioned atomic packing factor (APF) earlier in this article. This is an important concept in your introductory materials science class, so if you want a full explanation of APF, check out this page.

If you’re interested in advanced crystallography or crystallography databases, you may want to check out the AFLOW crystallographic library.

For a great reference for all crystal structures, check out “The AFLOW Library of Crystallographic Prototypes.”

The 14 Basic Crystal Structures

If you want to learn about specific crystal structures, here is a list of my articles about Bravais lattices and some related crystal structures for pure elements. Body-Centered Orthorhombic is one of these 14 Bravais lattices and also occurs as a crystal structure.

1. Simple Cubic
2. Face-Centered Cubic
2a. Diamond Cubic
3. Body-Centered Cubic
4. Simple Hexagonal
4a. Hexagonal Close-Packed
4b. Double Hexagonal Close-Packed (La-type)
5. Rhombohedral
5a. Rhombohedral Close-Packed (Sm-type)
6. Simple Tetragonal
7. Body-Centered Tetragonal
7a. Diamond Tetragonal (White Tin)
8. Simple Orthorhombic
9. Base-Centered Orthorhombic
10. Face-Centered Orthorhombic
11. Body-Centered Orthorhombic
12. Simple Monoclinic
13. Base-Centered Monoclinic
14. Triclinic

Other articles in my crystallography series include:

Introduction to Bravais Lattices
What is the Difference Between “Crystal Structure” and “Bravais Lattice”
Atomic Packing Factor
How to Read Miller Indices
How to Read Hexagonal Miller-Bravais Indices
Close-Packed Crystals and Stacking Order
Interstitial Sites
Primitive Cells
How to Read Crystallography Notation
What are Point Groups
List of Point Groups
What are Space Groups
List of Space Groups
The 7 Crystal Systems