Primitive Unit Cells (including Wigner–Seitz and voronoi cells)

Written by Brandon Ohl in Crystallography,Crystallography Basics Last Updated November 24, 2022

If you’re googling “primitive cell,” I imagine you are a somewhat advanced student in materials science (or an extremely advanced PhD student in chemistry or physics?).

The primitive cell, or primitive lattice, is the smallest way to define a crystal cell or lattice.

Before you can understand primitive cells, first you need to understand the conventional cells. If you don’t know the “regular” crystal cells like FCC or BCC, I recommend you start with this article.

If you’re still here, I’ll assume you know some basics of crystals. For example, you know that the BCC unit cell has 2 atoms per cell in the traditional way of drawing the cell. It’s possible, however, to redraw the BCC crystal structure with only 1 atom per cell. 

This redrawn perspective is called the primitive cell. The concept is more theoretical in nature and is more difficult for most people to grasp because it hides some of the symmetry that is shown in the traditional way of drawing the BCC cell.

In this article, I’ll explain why the primitive cell is useful, list them for common conventional unit cells, and also show you the Wigner-Sietz way to construct any unit cell.

Outline

What are Crystals and the Unit Cell

Since this topic is geared towards more-advanced students, I’ll hide a refresher about crystals in collapsable text. If you want a full introduction to crystallography, you may want to read this article.

Click here to learn about unit cell definitions!

As you know, a crystal is made of a lattice + basis. The basis is the thing which is repeated (atoms, in our case), and the lattice is the pattern in which it is repeated. Here’s a 1-dimensional crystal.

The conventional way of identifying the unit cell is to draw it so that atoms are split evenly among different crystals. For example, in the image below, both the red box and blue box are valid depictions of the unit cell (in fact, any box of the same size would be a valid description).

However, the box I’ve drawn in red is more conventional, because it helps us remember that the crystal should repeat.

Take a look at this second example, with atoms spaced farther apart. In this case, if you drew the lattice to exactly encapsulate one atom (shown in blue), it would not make a unit cell. Draw another box to the right, and you’ll see that the two are not the same.

However, if you draw the box so that the left edge of the box contains half of one atom, and the right edge of the box contains half of a different atom, the spacing is always correct. The starting point does not matter, so you could redefine the unit cell as a rectangle with an atom in the center and empty space on both sides, but we usually leave it as I show with the red box.


There are many (actually, infinite) ways to draw the same crystal structure, but materials scientists usually use a certain convention. We typically draw the unit cell as the smallest cell that shows full symmetry, basing this structure on its underlying Bravais lattice.

Another, less common way to draw the unit cell is to draw it as small as possible, hiding symmetry relationships if necessary. Drawing the unit cell like this is called the primitive cell.

Definition of the Primitive Cell

Let’s start with a 2-dimensional example of a conventional cell vs its primitive cell.

This is a centered rectangular Bravais lattice. Since the basis is simply one atom, we can also say that it is a centered rectangular crystal. There is ¼ of an atom on each corner of the rectangle, and 1 full atom in the center.

This gives us 2 atoms per unit cell, and each unit cell has a volume of a\cdot b.

This way of looking at the unit cell tells you the full symmetry. Atoms are closer together in the vertical direction compared to the horizontal direction, and there is a centering operation as well. In a real material, this kind of information about atoms can provide all sorts of clues about the material properties.

Now, look at the exact same crystal structure. None of the atoms have moved, but we are visualizing it differently. (Spoiler, this is the primitive cell). Instead of a rectangle, imagine that we have a rhombus. The sides are the same length, but the angle is not 90º.

Now, we have 1 atom per unit cell (it’s not exactly ¼ of an atom on each of the 4 corners, but it still adds up to 1 atom in total). The number of atoms per unit area hasn’t changed since we have the exact same crystal, so the area of this new unit cell must be smaller than the old one. 

Specifically, the conventional unit cell had 2 atoms per cell, and the primitive one has 1 atom per cell. Therefore, the primitive unit cell has half the area of the conventional one.

Since the new unit cell has only 1 atom per cell, it is the smallest possible cell. Therefore, it is the primitive cell. 

Does that mean all primitive cells must have a single atom inside? Not necessarily.

Remember, there is a difference between “lattice point” and “atom.”

For every Bravais lattice, there exists a primitive lattice with a single lattice point in each cell. However, in a real crystal, each “lattice point” may be composed of multiple atoms.

For example, one of the most-common crystal structures is hexagonal close-packed (HCP). The HCP crystal is similar to the hexagonal Bravais lattice, except the HCP crystal has two atoms per lattice point. 

The hexagonal prism can be sliced into parallelepipeds. If you are talking about the Bravais lattices, the conventional hexagonal lattice has 3 lattice points. If you looked at the primitive hexagonal lattice, there is only 1 lattice point.

If you are talking about the HCP crystal structure, the conventional HCP unit cell has 6 atoms, while the primitive HCP unit cell has 2 atoms.

I hope that illustrates how a primitive crystal cell can have more than one atom per unit cell, but a primitive Bravais lattice must have only 1 lattice point.

In fact, you have probably even seen an HCP primitive cell before.

Primitive Versions of Conventional Unit Cells and Bravais Lattices (List)

You just saw the primitive cell for the HCP crystals, and the primitive lattice for the hexagonal lattice, but I’ll repeat them for the folks that skipped straight to this section.

Primitive Hexagonal Close-Packed

The primitive hexagonal lattice is the easiest to see, in my opinion. Take a vertical slice through ⅓ of the conventional cell, and there you have it! The hexagonal primitive lattice has 1 lattice point spread through the 8 corners of the parallelpiped.

The crystal structure corresponding to the hexagonal Bravais lattice, the Simple Hexagonal crystal structure, does occur in nature (for example, graphite). However, the Hexagonal Close-Packed (HCP) crystal is much more common.

The HCP primitive cell is a parallelpiped with 2 atoms inside. One atom is spread through the 8 corners, and the other atom rests in the center.

The primitive hexagonal cell can be described by the vectors:

\vec{a}_1=\frac{a}{2}\hat{x}-\frac{\sqrt{3}a}{2}\hat{y}
\vec{a}_2=\frac{a}{2}\hat{x}+\frac{\sqrt{3}a}{2}\hat{y}
\vec{a}_3=c\hat{z}

And the basis:

B_{1}=\frac{a}{2}\hat{x}+\frac{1}{2\sqrt{3}}a\hat{y}+\frac{1}{4}c\hat{z}
B_{2}=\frac{a}{2}\hat{x}-\frac{1}{2\sqrt{3}}a\hat{y}+\frac{3}{4}c\hat{z}

Primitive Cubic

The Simple Cubic (SC) crystal structure is already a primitive cell. Yes, in many cases, the conventional cell is the primitive cell. Usually, the reason why we use a conventional cell is that the primitive cell doesn’t show full symmetry. In this case, the primitive SC cell does show full symmetry, so it is also the conventional cell. In fact, another name for Simple Cubic is “Primitive Cubic.”

Primitive cell of Simple Cubic (SC) Bravais Lattice can be described by vectors:

\vec{a}_{1}=a\hat{x}
\vec{a}_{2}=a\hat{y}
\vec{a}_{3}=a\hat{z}

The volume of this cell is V=a^3

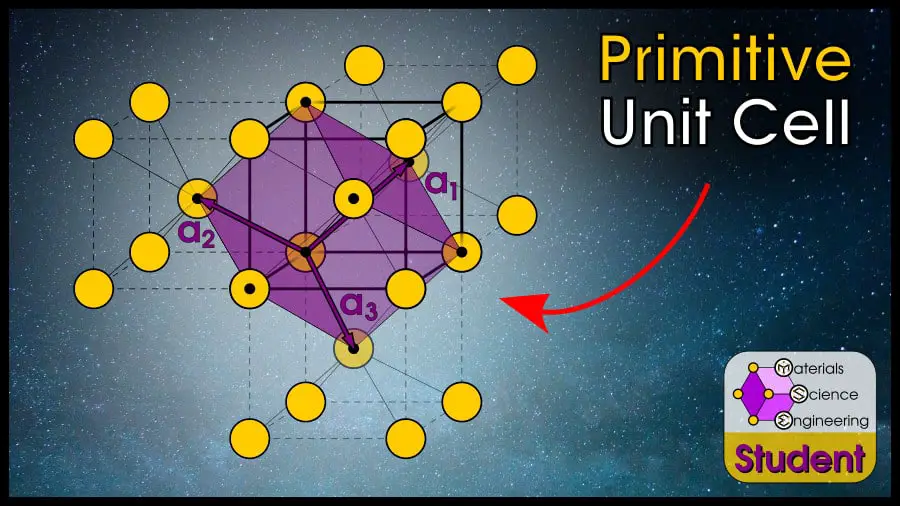
Primitive Face-Centered Cubic (FCC)

The Face-Centered Cubic (FCC) crystal structure is the crystal structure with 1 atom at each lattice point in the FCC Bravais lattice.

To find the primitive cell, start with an atom as one corner of your cell, then find the 7 closest atoms which will make up the other corners. In theory, you could choose any random shape as long as it completely tiles 3D space and has a volume such that there is one atom per cell (there are infinite possibilities for primitive cells), but the easiest FCC primitive cell is shown below.

Primitive cell of Face-Centered Cubic (FCC) Bravais Lattice can be described by vectors:

\vec{a}_{1}=\frac{a}{2}\hat{y}+\frac{a}{2}\hat{z}
\vec{a}_{2}=\frac{a}{2}\hat{x}+\frac{a}{2}\hat{z}
\vec{a}_{3}=\frac{a}{2}\hat{x}+\frac{a}{2}\hat{y}

The volume of this cell is V=\frac{a^3}{4}

This cell has 3 side lengths equal to each other 2r and the three vectors have 120º angles to each other.

The volume of the primitive cell is V=\frac{a^3}{4}, or ¼ the volume of the conventional FCC unit cell. You can find this number using geometry calculations, or by using the knowledge that the primitive cell has the same atoms/volume as the conventional cell, and since the conventional cell has 4 times as many atoms per cell, the primitive cell must have ¼ the volume.

Primitive Body-Centered Cubic (BCC)

To find the BCC primitive cell, you can use the same method I discussed for FCC. The result is shown below:

Primitive cell of Body-Centered Cubic (BCC) Bravais Lattice can be described by vectors:

\vec{a}_{1}=-\frac{a}{2}\hat{x}+\frac{a}{2}\hat{y}+\frac{a}{2}\hat{z}
\vec{a}_{2}=\frac{a}{2}\hat{x}-\frac{a}{2}\hat{y}+\frac{a}{2}\hat{z}
\vec{a}_{3}=\frac{a}{2}\hat{x}+\frac{a}{2}\hat{x}-\frac{a}{2}\hat{z}

The volume of this cell is V=\frac{a^3}{2}

The primitive BCC unit cell is defined by 3 vectors which have the same length of 2r, with two angles = 90º and one angle = 2\tan^{-1}({\frac{1}{\sqrt{2}}}) or 70.53º. There is 1 atom per unit cell.

The volume of the primitive BCC unit cell, V=\frac{a^3}{2}, is ½ the volume of the conventional BCC unit cell.

Primitive Hexagonal

You already saw the primitive HCP cell, and the primitive hexagonal cell follows the same principle.

The primitive vectors are:

\vec{a}_1=\frac{a}{2}\hat{x}-\frac{\sqrt{3}a}{2}\hat{y}
\vec{a}_2=\frac{a}{2}\hat{x}+\frac{\sqrt{3}a}{2}\hat{y}
\vec{a}_3=c\hat{z}

The volume of this cell is V=(\frac{\sqrt{3}}{2})a^2c

Primitive Rhombohedral

The conventional simple rhombohedral unit cell is already primitive and has 1 atom per unit cell.

The primitive vectors are:

\vec{a}_{1}=a(1+\phi)\hat{x}+a\hat{y}+a\hat{z}
\vec{a}_{2}=a\hat{x}+a(1+\phi)\hat{y}+a\hat{z}
\vec{a}_{3}=a\hat{x}+a\hat{y}+a(1+\phi)\hat{z}

where \phi is between -\frac{1}{6} and \frac{1}{3}.

The volume of this cell is V=(\frac{2}{\sqrt{3}})a^2c

Primitive Tetragonal

The conventional simple tetragonal unit cell is already primitive and has 1 atom per unit cell.

The primitive vectors are:

\vec{a}_1=a\hat{x}
\vec{a}_2=a\hat{y}
\vec{a}_3=c\hat{z}

The volume of this cell is V=a^2c

Primitive Body-Centered Tetragonal (BCT)

The primitive BCT unit cell resembles the primitive BCC unit cell, since it looks like BCC but with one side having a different length than the others.

The primitive BCT unit cell has a=b, c and \alpha=\beta, \gamma. The volume of a tetragonal cell is given by V=\frac{a^2c}{2}, and since the primitive BCT cell has 1 atom compared to 2 in the conventional BCT cell, the the primitive BCT unit cell has half the volume of the conventional BCT unit cell.

The lattice vectors for a primitive BCT cell are:

\vec{a}_1=-\frac{a}{2}\hat{x}+\frac{a}{2}\hat{y}+\frac{c}{2}\hat{z}
\vec{a}_2=\frac{a}{2}\hat{x}-\frac{a}{2}\hat{y}+\frac{c}{2}\hat{z}
\vec{a}_3=\frac{a}{2}\hat{x}+\frac{a}{2}\hat{y}-\frac{c}{2}\hat{z}

The volume of this cell is V=\frac{a^2c}{2}

Primitive Orthorhombic

The conventional simple orthorhombic unit cell is already primitive and has 1 atom per unit cell.

The primitive vectors are:

\vec{a}_{1}=a\hat{x}
\vec{a}_{2}=b\hat{y}
\vec{a}_{3}=c\hat{z}

The volume of this cell is V=abc

Primitive Face-Centered Orthorhombic

The primitive face-centered orthorhombic unit cell resembles the FCC primitive cell, although the three sides are not equal to each other.

The primitive vectors are:

\vec{a}_{1}=\frac{b}{2}\hat{y}+\frac{c}{2}\hat{z}
\vec{a}_{2}=\frac{a}{2}\hat{x}+\frac{c}{2}\hat{z}
\vec{a}_{3}=\frac{a}{2}\hat{x}+\frac{b}{2}\hat{y}

The volume of this cell is V=\frac{abc}{4}

Primitive Body-Centered Orthorhombic

The primitive body-centered orthorhombic unit cell resembles the BCC and BCT primitive cells, but this time all three sides have different lengths.

The primitive vectors are:

\vec{a}_{1}=-\frac{a}{2}\hat{x}+\frac{b}{2}\hat{y}+\frac{c}{2}\hat{z}
\vec{a}_{2}=\frac{a}{2}\hat{x}-\frac{b}{2}\hat{y}+\frac{c}{2}\hat{z}
\vec{a}_{3}=\frac{a}{2}\hat{x}+\frac{b}{2}\hat{x}-\frac{c}{2}\hat{z}

The volume of this cell is V=\frac{abc}{2}

Primitive Base-Centered Orthorhombic

The primitive cell for base-centered orthorhombic is actually easy to see, if you remember the trick for finding the primitive cell of the 2D centered rectangular lattice.

The primitive vectors are:

\vec{a}_{1}=\frac{a}{2}\hat{x}-\frac{b}{2}\hat{y}
\vec{a}_{2}=\frac{a}{2}\hat{x}+\frac{b}{2}\hat{y}
\vec{a}_{3}=c\hat{z}

The volume of this cell is V=\frac{abc}{2}

Primitive Monoclinic

The conventional monoclinic unit cell is already primitive and has 1 atom per unit cell.

The primitive vectors are:

\vec{a}_{1}=a\hat{x}
\vec{a}_{2}=b\hat{y}
\vec{a}_{3}=c\cos{\beta}\hat{x}+c\sin{\beta}\hat{z}

The volume of this cell is V=abc\sin{\beta}

Primitive Base-Centered Monoclinic

The primitive cell for base-centered monoclinic can be visualized using the same trick as base-centered orthorhombic or the 2D centered rectangular cells.

The primitive vectors are:

\vec{a}_{1}=\frac{a}{2}\hat{x}-\frac{b}{2}\hat{y}
\vec{a}_{2}=\frac{a}{2}\hat{x}+\frac{b}{2}\hat{y}
\vec{a}_{3}=c\cos{\beta}\hat{x}+c\sin{\beta}\hat{z}

The volume of this cell is V=(\frac{1}{2})abc\sin{\beta}

Primitive Triclinic

The conventional triclinic unit cell is already primitive and has 1 atom per unit cell.

The primitive vectors are:

\vec{a}_{1}=a\hat{x}}
\vec{a}_{2}=b\cos{\gamma}\hat{x}+b\sin{\gamma}\hat{y}
\vec{a}_{3}=c_x\hat{x}+c_y\hat{y}+c_z\hat{z}

where

c_x=c\cos{\beta}
c_y=\frac{c(\cos{\alpha}-\cos{\beta}\cos{\gamma})}{\sin{\gamma}}

and

c_z=\sqrt{c^2-c_x^2-c_y^2}

The volume of this cell is V=abc_z\sin{\gamma}

Wigner-Seitz and Voronoi

So far we have constructed primitive cells using a mixture of intuition and guess-and-check (or you just peeked at the answer).

The primitive cells I’ve shown you so far are the standard primitive cells–they don’t have the full symmetry of the non-primitive conventional cells, but they are built to be similar to conventional cells.

There is another method of using math to generate a different set of primitive cells (remember, each primitive cell is one of infinite ways to describe the same pattern).

The primitive cells created by this method are called Wigner-Seitz unit cells. 

Rather than splitting the atom to put ⅛ of it on each of the 8 corners, the Wigner-Seitz unit cell has a single atom surrounded by empty space. 

Wigner-Seitz cells are unique, but they are not that intuitive to understand as a crystal structure. However, the algorithm to create these cells is simple. Let’s start with an example in 2D.

  1. Choose any lattice point to start. This atom will be the only atom to appear in the cell, and it will be exactly in the center.
  1. Draw a line from your center atom to every other atom. You’ll see that most of these will be redundant, so in practice you only need to draw lines to the close atoms. We’ll color these lines red.
  1. Find the midpoint of each red line.
  1. From the midpoint, draw a blue line perpendicular to the red line. The blue lines should be infinitely long.
  1. The perpendicular blue lines will form the outline of a polygon. The smallest polygon formed is the primitive cell.

If you’ve done this correctly, your polygon should completely fill the space!

What I have described is an algorithm for creating Voronai polygons. Voronai polygons are a mathematical concept which describes the set of all space which is closer to one point than any other.

The Wigner-Seitz unit cell is the unit cell which is generated from the voronai technique. There are also Voronai polyhedra, which are the 3-dimensional equivalent.

When making 3D Wigner-Seitz cells, use the same procedure that I outlined. However, instead of drawing blue lines perpendicular to the red lines, draw blue planes perpendicular to the red lines.

The planes which intersect to form the smallest polyhedron is your Wigner-Seitz cell!

However, a note of caution: the method of generating Wigner-Seitz primitive cells only works when you center the cell around a lattice point. 

Final Thoughts

Primitive cells or primitive lattices are the best way to describe atomic crystal structures with math. Primitive cells are the smallest possible cell. There are an infinite number of primitive cells, but materials scientists typically use one of two types: the conventional primitive lattice has ⅛ of a  lattice point at each corner of a parallelepiped, and the Wigner-Seitz primitive cell has a lattice point at the center of each polyhedron.

References and Further Reading

AFLOW library is a great resource for primitive cells, external to this site.

If you want to see the other crystallography-related articles I’ve written, here is this list, in recommended reading order:

Introduction to Bravais Lattices
What is the Difference Between “Crystal Structure” and “Bravais Lattice”
Atomic Packing Factor
How to Read Miller Indices
How to Read Hexagonal Miller-Bravais Indices
Close-Packed Crystals and Stacking Order
Interstitial Sites
Primitive Cells
How to Read Crystallography Notation
What are Point Groups
List of Point Groups
What are Space Groups
List of Space Groups
The 7 Crystal Systems

If you are interested in more details about any specific crystal structure, I have written individual articles about simple crystal structures which correspond to each of the 14 Bravais lattices:

1. Simple Cubic
2. Face-Centered Cubic
2a. Diamond Cubic
3. Body-Centered Cubic
4. Simple Hexagonal
4a. Hexagonal Close-Packed
4b. Double Hexagonal Close-Packed (La-type)
5. Rhombohedral
5a. Rhombohedral Close-Packed (Sm-type)
6. Simple Tetragonal
7. Body-Centered Tetragonal
7a. Diamond Tetragonal (White Tin)
8. Simple Orthorhombic
9. Base-Centered Orthorhombic
10. Face-Centered Orthorhombic
11. Body-Centered Orthorhombic 
12. Simple Monoclinic 
13. Base-Centered Monoclinic 
14. Triclinic

Recommended Posts