What Are Bravais Lattices? (Definition, Types, Examples)

Bravais lattices are a way to describe a repeating arrangement of objects that fill a space. Bravais lattices are the foundation for crystal structures

Bravais lattices are the basic lattice arrangements. All other lattices can simplify into one of the Bravais lattices. Bravais lattices move a specific basis by translation so that it lines up to an identical basis. In 3 dimensions, there are 14 Bravais lattices:

Simple Cubic
Face-Centered Cubic
Body-Centered Cubic
Hexagonal
Rhombohedral
Simple Tetragonal
Body-Centered Tetragonal
Simple Orthorhombic
Face-Centered Orthorhombic
Body-Centered Orthorhombic
Base-Centered Orthorhombic
Simple Monoclinic
Base-Centered Monoclinic
Triclinic

Bravais lattices assume that the basis is reduced to a single point (I’ll go over examples later in the article). Since atoms are also a single point, many pure elements have a crystal structure which is the same as its Bravais lattice.

To know which Bravais lattice fits a certain pattern, check for translational symmetry. If you can exactly repeat the entire structure by a set of translations, that is the lattice. Another way to think about it is that an infinite lattice is exactly the same, regardless of which particular point you start at.

It is also possible to have larger lattices than the most-basic lattice. The smallest-possible unit cell is called the “primitive” unit cell, but in many cases it’s more natural to use a larger unit cell which shows full symmetry.

For example, the hexagonal Bravais lattice can be simplified into a rhombus, but this image doesn’t show the full symmetry.

Finally, here is a mathematical description of lattice points in a Bravais lattice.

Click here to expand!

For 1D: $\vec{R}=n_{1}\vec{V_{1}}$
For 2D: $\vec{R}=n_{1}\vec{V_{1}}+n_{2}\vec{V_{2}}$
For 3D: $\vec{R}=n_{1}\vec{V_{1}}+n_{2}\vec{V_{2}}+n_{3}\vec{V_{3}}$
For 4D: $\vec{R}=n_{1}\vec{V_{1}}+n_{2}\vec{V_{2}}+n_{3}\vec{V_{3}}+n_{4}\vec{V_{4}}$

$n$ is an integer, and $V$ are the vectors. This is just a description of real space (that’s why it says $R$ ).

The vectors can’t be parallel, and the scalars are normalized. For example, suppose you had a lattice of points that formed a bunch of rectangles.

We can define V₁ and V₂ as these two vectors. They could be any length, but let’s just assume that V₁ is 10 mm and V₂ is 15 mm. These vectors are at right angles to each other. If you traveled along V₁, you’d see an atom every 10 mm. You would only see an atom at multiples of 10 mm.

The Bravais lattices are constructed by considering the unique combination of vectors such that every lattice point can be described by translation (mathematically, an integer times a vector is just translation).

For example, in 1-dimension there is only 1 possible Bravais lattice. Space extends in 1 direction (V₁), and the lattice must repeat along that one direction. Since there is only 1 vector, there can only be 1 Bravais lattice.

The Bravais lattices are distinguished by the vectors. Are the vectors the same size? Do the vectors have the same angles to each other? The “important” angles are determined by symmetry. For example, a square means 2 vectors are the same length and are at 90° to each other.

Should 90° be different than 89°? Yes, because a square has 4-way rotational symmetry but a rhombus only has 2-way rotational symmetry.

Should 89° be different than 88°? No, because both cases are rhombuses with 2-way rotational symmetry.

In 2-dimensions, there are 5 possible Bravais lattices. Space extends in 2 directions, so:

V₁ and V₂ are the same length and have a 90 degree angle
V₁ and V₂ are the same length and have a 120 degree angle
V₁ and V₂ are the same length and have an angle which is not 90 or 120 degrees.
V₁ and V₂ have different lengths and a 90 degree angle
V₁ and V₂ have different lengths and an angle which is not 90 degrees

A lattice of triangles, for example, would not work without rotation. But you could combine six triangles and get a hexagon, which can fully tile a space without rotation.

If you tried to define some other lattice in 2-dimensions, it would always be possible to simplify it into one of the five I just mentioned. I’ll walk through a few of these examples in the 1D and 2D lattice sections later in the article.

By the way, so I don’t confuse you: in this math-y section I’ve used V₁, V₂, V₃,…V_n to show you how this can be generalized for an infinite number of dimensions, but real life has 3 dimensions. Lattices are usually described with vectors named a, b, and c.

Outline

Why Bravais Lattices Matter in Crystallography
1D Bravais Lattice
2D Bravais Lattices
3D Bravais Lattices
Primitive Cells
Space Groups and Point Groups
Bravais Lattices vs Crystal Groups
Final Thoughts
References and Further Reading

Why Bravais Lattices Matter in Crystallography

Crystal structures are defined by a lattice and basis. The basis is what gets repeated in the crystal structure. The lattice is how it gets repeated. (For a refresher on what crystals are, here is a basic introduction).

Basically, most materials are crystals, and crystals have a repeating pattern of atoms. Bravais lattices describe the basic crystal structure (there are also point groups and space groups but I’ll discuss them later).

The basic crystal structure can make a huge difference in a material’s property. Here is an entire article explaining the differences between Face-Centered Cubic and Body-Centered Cubic crystal structures.

1D Bravais Lattice

There is only 1 bravais lattice in 1-dimension. Actually talking about this is trivial, but I think it’s the easiest way to see how more-complex arrangements collapse into the basic bravais lattices.

There is only 1 direction, so if something will repeat, it must repeat at a certain distance in that direction. There is only 1 variable (the distance something will repeat) so there is only 1 lattice. We can call this the “linear” Bravais lattice.

Imagine that you wanted to design a 1-D pattern that was more complicated than just a series of identical dots. How about, instead, we create a pattern of multicolored dots with mirror symmetry?

What we have actually done is created a complicated basis. The lattice symmetry doesn’t change. There is still some distance at which this pattern repeats itself. This distance is larger than with a single-circle basis, but it still exists (if it didn’t repeat, it wouldn’t be a lattice at all).

When we reduce the complicated basis to a single point, the translational symmetry remains unchanged.

Remember, bravais lattices only consider translational symmetry. If you wanted to consider other symmetrical relationships like reflection, rotation, or inversion, you’d need point groups and space groups.

2D Bravais Lattices

There are five basic 2D Bravais lattices.

Square, a=b, θ=90°
Hexagonal, a=b, θ=120°
Rectangular, a≠b, θ=90°
Centered Rectangular
1. Note the primitive cell is like hexagonal or square but less symmetry
2. Note: only centered, not face body or base
Rhomboidal, a≠b, θ≠90°

If you tried to think of another pattern that fully covered a 2D space, such as centered square or off-centered rectangular, it could be reduced to one of these 5 2D lattices. A mathematician might like to prove this, but as an engineer I accept that the proof has already been performed. But I encourage you to think of a few examples of more complex arrangements, and consider which basic lattice you have.

For example, you may notice that there is a centered-rectangular lattice, but not a centered-square lattice. That’s because if you added a centered atom to the square lattice, it would actually still be a square lattice, but smaller.

On the other hand, adding a centered atom to rectangular means that the new crystal has a parallelogram-shaped lattice with a=b and θ ≠ 90°. Similarly, adding a centered atom to this lattice would give you back a rectangular lattice. Because rectangles have higher symmetry I prefer to describe them as rectangular and centered-rectangular lattices.

I bring up the 2D lattices because I want to give you an opportunity to play with them in your head. Once we get to complicated 3D lattices, which matter because of crystallography, you’ll probably just have to take my word that these are all 14 possible lattices.

Square

The square 2D Bravais lattice completely tiles a space with squares. The vectors a and b are equal to each other and are at right angles.

Hexagonal

The hexagonal 2D Bravais lattice might also be described as rhombic. You may like to think of them as triangular, although it actually requires 2 triangles (one up, the other down) to maintain translational symmetry.

This lattice tiles a space with hexagons or rhombuses (I prefer “hexagonal” because it indicates higher symmetry). The vectors a and b are equal to each other and at an angle of 120.

(In principle, the hexagonal Bravais lattice is a subset of the centered-rectangular lattice, but it gets a special name because the perfect 120° angle has higher symmetry and makes hexagons).

Rectangular

The rectangular 2D Bravais lattice tiles a space with rectangles. The vectors a and b are a at right angles but have different magnitudes.

Notice that another way to imagine this lattice is if you had a and b with the same length, but not at right angles, with another lattice point in the center.

I mention this just to help you think of the relationships between lattices, and how easily two seemingly-different lattices might end up being identical.

Centered-Rectangular

The centered-rectangular 2D Bravais lattice tiles a space with rectangles that have an extra lattice point in the center. The vectors a and b are at right angles and have different lengths; one extra point is at the center.

You may realize that it’s possible to make a different lattice without requiring an atom in the center.

This lattice has vectors a and b of the same length, at non-90° angles.

From one perspective, this lattice is simpler than the original one I showed you, because the unit cell has less area and lattice points inside. Since this one is the simplest possible lattice, we call it the primitive lattice.

However, this depiction of the primitive lattice does not show the full symmetry, so we tend to use the non-primitive, centered-rectangular depiction instead.

Rhomboidal (Oblique)

The rhomboidal 2D Bravais lattice tiles a space with rhomboids. This lattice has vectors a and b of different lengths at non-90° angles.

This lattice is actually called “oblique” in most places I looked, but I thought it would make more sense if I actually called it by the proper shape. Rhomboids are parallelograms with non-90° angles and 2 different side lengths. There is no such 2D shape as “oblique.”

Click here to see more examples!

Let’s look at a few more complex patterns and see if you can identify the Bravais lattice.

Remember that Bravais lattices are the result of simplifying a basis to a single point. If the basis is a single atom, that’s trivial. If the basis is multiple atoms (or something more complex, like a pattern in a painting) this may get trickier.

This example may seem familiar to you:

You might think this is hexagonal, but the lattice seems to be shaped like a squished hexagon. Additionally, the hexagonal lattice has an extra atom in the center of each hexagon.

If you consider each yellow dot to be a lattice point, then this is not a Bravais Lattice. The bravais lattices are the simplest lattices.

Instead, you could collapse multiple yellow dots into a single lattice point. There are many ways to do this, but the simplest for me to see is to consider each squashed hexagon (with 6 pieces of ⅙ different dots) as one lattice point. I’ve represented the new lattice point as a purple dot.

With purple dots, you can see that the lattice has restored the point in the middle of the hexagon. However, the hexagon is still squashed and doesn’t have a perfect 120° angle, so by the rules I showed earlier this has a centered rectangular underlying lattice.

Finally, here is an example which doesn’t use circles. Crystals and lattices can appear in many forms. Any time you have some region which can be perfectly translated onto a copy of itself, you have a crystal. The region is the basis, and the possibilities for translation are the Bravais lattice.

Take a look at this tessellation I made, inspired by one of M.C. Escher’s sketches. Can you identify a lattice and basis?

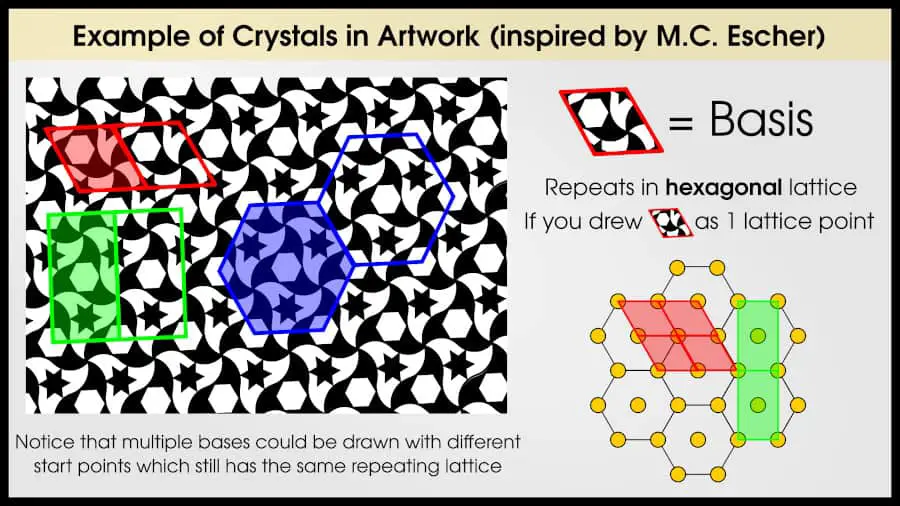
There are any number of bases you could choose, but I’ve picked out three. In red, I’ve drawn a rhombus which has the smallest area of the three I chose. You can see that this area perfectly repeats if you translate it up, down, left, or right. I drew the rhombus with a black star at each corner, but the same translational symmetry shows up no matter where I place the start point of the rhombus.

You can also see I’ve found a hexagon-shaped basis which repeats in 6-directions. (Remember that the hexagonal and rhomboidal lattices are the same.)

Finally, I drew a rectangular centered basis. If you look at the hexagonal 2D lattice, you’ll notice that it’s always possible to identify a rectangular centered lattice, since a rectangular centered lattice is a precondition for the hexagonal lattice.

3D Bravais Lattices

Now we get into the Bravais lattices which are useful to materials science. There are 14 3D Bravais lattices. Remember that the Bravais lattices come by considering translational symmetry. Other symmetries, like reflection or inversion, are captured in point groups and space groups, not Bravais lattices.

I’ll provide a short description of each lattice, and list some common materials with that structure. For a more in-depth look at each kind of lattice, I have written a dedicated article for each one. You can find those linked at the top or bottom of this article.

Each lattice is a polyhedron with 6 faces, 12 edges, and 8 vertices. We can describe these polyhedrons using 3 vectors which correspond to 3 of the 12 edges (because of the 4-sided nature of the polygon, there will be 3 sets of 4 matching edges. That’s why we only need to describe 3 different vectors, as long as they come from 3 different edge sets).The cube is the highest-symmetry lattice shape. All 12 edges are the same length and they all have the same angle to each other (90°), which can be represented as 3 vectors of identical length, at 90° to each other.

In addition to having a lattice point at each vertex of the polyhedron, there may also be “centering.” Centering could mean there is an extra atom at the center of the entire polyhedron, at the center of each of the 6 faces, or at the center of the top and bottom faces (base).

For example, if a lattice had a lattice point at each corner of a cube, plus another lattice point at each face of the cube, it would be called “face-centered cubic” and abbreviated cF (c for cubic, F for face-centered).

If the cube had an extra lattice point on the top and bottom faces (not all 6) it would be called “base-centered cubic) and abbreviated cC (c for cubic, C for base-centered. I noticed that wikipedia’s article uses S for base-centered; whoever wrote that must have used a different textbook than me). Note, however, that base-centered cubic doesn’t exist because it can just be redrawn as simple tetragonal.

If the cube had an extra lattice point in the very center, it would be “body-centered cubic” and abbreviated cI (c for cubic, I for body-centered).

The Bravais lattices can be cubic, rhombohedral/hexagonal, or variations of a cube with different side lengths (monoclinic, orthorhombic, tetragonal, and triclinic).

The lattices can have an extra lattice point on all the faces (F), the top and bottom bases (C), or the center (I). If there are no extra lattice points, the lattice is called “simple” or “primitive” (P).

By combining the 7 possible polyhedrons with 4 possible centerings and crossing off duplicates, you end up with 14 Bravais lattices.

Simple Cubic

The Simple Cubic Bravais lattice, also called “primitive cubic,” is a cube 3 vectors of the same size at 90° to each other.

As a crystal structure, simple cubic has a very low packing density, so it is rare. Polonium is one of the only materials that has a simple cubic crystal structure.

You may see simple cubic abbreviated as SC or cP.

Face-Centered Cubic

The Face-Centered Cubic (FCC) Bravais lattice is a cube with 3 vectors of the same size at 90° to each other. There is an additional lattice point at the face of each side. The Face-Centered Cubic crystal structure may also be called “cubic close-packed” (CCP). CCP is more common to see in older textbooks–the idea was to distinguish the CCP crystal (basically FCC lattice with 1-atom basis) from the FCC lattice. Nowadays, FCC is the more popular term for both the crystal structure and Bravais lattice.

As a crystal structure, FCC has a very high packing density, so it is common. Nickel and copper are just two elements that have this crystal structure.

You may see Face-Centered Cubic abbreviated as FCC, CCP, or cF.

Body-Centered Cubic

The Body-Centered Cubic (BCC) Bravais lattice is a cube with 3 vectors of the same size at 90° to each other. There is an additional lattice point at the center of the cube.

As a crystal structure, BCC has a high packing density, so it is common. Iron and tungsten are just two elements that have this crystal structure.

You may see Body-Centered Cubic abbreviated as BCC or cI.

Simple Hexagonal

If you come from a materials science background, you may be used to seeing the Hexagonal Close-Packed (HCP) crystal structure. HCP is a crystal structure with a more complicated basis–the underlying Bravais lattice is Simple Hexagonal.

The Hexagonal Bravais lattice is a hexagonal prism. The prism can also be constructed from a primitive cell which is a parallelepiped. Two vectors for the base have the same length and are at 120° to each other. The third vector is at 90° to the first two, but has a different length.

As a crystal structure, this lattice may be called “Simple Hexagonal” (SH) or “primitive hexagonal” to emphasize that the crystal structure has a 1-atom basis. However, more common crystal structures based on the hexagonal Bravais lattice include Hexagonal Close-Packed (HCP) and Double Hexagonal Close-Packed (DHCP).

As a crystal structure, simple hexagonal has a low packing density, so it is not very common. Its denser, more-common counterparts, HCP and DHCP, technically still have the hexagonal Bravais lattice though, so these elements include carbon, lanthanum, and cobalt.

You may see Simple Hexagonal abbreviated as SH or hP.

Rhombohedral

The Rhombohedral Bravais lattice is like a cube, but the corners aren’t at 90°. There are 3 vectors of the same size at the same non-90° angle to each other.

Since there can’t be additional atoms in the faces or center, there is only “simple” rhombohedral (SR).

There are a few low-melting point elements with a rhombohedral crystal structure, such as mercury, antimony, and bismuth.

You may see Rhombohedral abbreviated as SR or hR.

Simple Tetragonal

The simple tetragonal Bravais lattice is an elongated cube. All 3 vectors are at 90° to each other, two are the same length, and the third has a different length.

As a crystal structure, simple tetragonal is not as stable as cubic crystals, but it’s generally more stable than monoclinic or triclinic crystals structures. Tin and indium both have tetragonal crystal structures, and it’s no coincidence that they melt at relatively low temperatures.

You may see simple tetragonal abbreviated as ST or tP.

Body-Centered Tetragonal

The Body-Centered Tetragonal (BCT) Bravais lattice is an elongated cube. All 3 vectors are at 90° to each other, two are the same length, and the third has a different length. It resembles the simple tetragonal lattice, but there is an extra point in the center.

There are very few elements with a natural BCT crystal structure. Indium is one of them. This crystal structure can also come from a stressed system. One extremely common example is martensite in steel. Martensite develops when iron is rapidly cooled from its FCC structure to its BCC structure. The lattice has stress which comes out in an elongated side of the cube, resulting in BCT instead of BCC.

You may see body-centered tetragonal abbreviated as BCT or tI.

Simple Orthorhombic

The Simple Orthorhombic (SO) Bravais lattice is like a cube with 3 different side lengths. All 3 vectors are at 90° to each other but each has a different length.

As a crystal structure, simple orthorhombic is not as stable as cubic crystals, but it’s generally more stable than monoclinic or triclinic crystals structures. Gallium, phosphorus, and bromine have orthorhombic crystal structures, and it’s no coincidence that they melt at relatively low temperatures.

You may see simple orthorhombic abbreviated as SO or oP.

Base-Centered Orthorhombic

The Base-Centered Orthorhombic Bravais lattice is ust like simple orthorhombic, but with an atom centered on the top and bottom faces.

There are no elements with a base-centered orthorhombic crystal structure at STP, but many minerals have crystal structures with a base-centered orthorhombic underlying Bravais lattice.

You may see base-centered orthorhombic abbreviated as oC.

Face-Centered Orthorhombic

The Face-Centered Orthorhombic (FCO) Bravais lattice is just like simple orthorhombic or base-centered orthorhombic, but with an atom centered on all 6 faces.

There are no elements with a face-centered orthorhombic crystal structure at STP, but many minerals have crystal structures with a FCO underlying Bravais lattice.

You may see base-centered orthorhombic abbreviated as FCO or oF.

Body-Centered Orthorhombic

The Body-Centered Orthorhombic Bravais lattice is just like simple orthorhombic, but with an atom centered at the center of the polyhedron.

There are no elements with a body-centered orthorhombic crystal structure at STP, but many minerals have crystal structures with a body-centered orthorhombic underlying Bravais lattice.

You may see base-centered orthorhombic abbreviated as oI.

Simple Monoclinic

The Simple Monoclinic (SM) Bravais lattice is a distorted cube. The 3 vectors are at different lengths. They make 2 right angle, and one non-right angle.

Simple monoclinic has even lower symmetry than the other Bravais lattices we’ve looked at so far, so it’s not common in pure elements at STP. The only example of a monoclinic crystal that appears on the periodic table is plutonium, a radioactive material.

You may see simple monoclinic abbreviated as SM or mP.

Base-Centered Monoclinic

Base-Centered Monoclinic (BCM) is just like monoclinic, but with an extra atom centered on the base (two faces on opposite sides).

There are no elements with a base-centered monoclinic crystal structure at STP, but some minerals have crystal structures with a base-centered monoclinic underlying Bravais lattice.

You may see base-centered monoclinic abbreviated as BCM or mC.

Triclinic

The triclinic Bravais lattice is the lattice with the least symmetry. It is a heavily distorted cube with 3 different edge lengths and angles which don’t match and are not at 90° to each other.

There are no elements with a triclinic crystal structure at STP, but some minerals have crystal structures with a triclinic underlying Bravais lattice.

You may see triclinic abbreviated as tP.

Primitive Cells

So far in this article, I’ve mentioned the term “primitive cell” or “primitive lattice” a few times.

The primitive lattice is the smallest lattice that can be made (thus, it must have only a single lattice point). I wrote an entire article about primitive cells, click here to check it out!

Whether you are talking about the conventional lattice or the primitive lattice, the lattice points remain unchanged. This is just a way of thinking about how they are arranged.

Since cells are composed of both a lattice and basis, the primitive cell is the unit cell that considers the primitive lattice, rather than the conventional lattice. Note that primitive cells can have more than 1 atom, because the basis could consist of multiple atoms.

Primitive cells are not usually taught to beginners in materials science, because crystallography is complicated enough when we use the intuitive unit cells.

However, since this article is an introduction to crystallography, I thought I should make you aware of it.

The most common primitive cell is the hexagonal close-packed (HCP) cell. HCP uses a hexagonal lattice with extra atoms.

As you can see, rather than dividing the cell into hexagonal prisms, you could divide it into smaller parallelepipeds (that’s the technical term for the smaller shape you see).

The parallelpiped unit cell has 1 lattice point (shared between the 8 corners), but since the HCP cell has a more complicated basis, there are 2 atoms in the HCP unit cell.

If you want to learn more about primitive cells, check out this article.

(Fun fact: this website was inspired because, in my undergraduate days, I could not find online answers for primitive cells or the difference between Wigner–Seitz cells and voronoi cells).

Space Groups and Point Groups

This article is about Bravais lattices, not space groups or point groups. Perhaps I’ll get around to writing a full course of Structures in Materials Science, but for now you’ll have to look elsewhere to find out more about space groups and point groups.

However, I would feel guilty if I didn’t at least explain the concept.

The Bravais lattices are the 14 ways to repeat lattice points to fill a space by translation. There are 14 Bravais lattices (in 3D).

The point groups are the ways to repeat lattice points using reflection, rotation, or rotoinversion. There are 32 crystallographic point groups. For more, check out this article about point groups.

The space groups are the unique combination of Bravais lattices and point groups. There are 230 unique space groups in 3D. (If you’re wondering why there are 230 space groups instead of 448, it’s because many of those 448 end up identical). Here you’ll find a simple explanation of space groups.

For a list of the 230 space groups, check out this post.

Bravais Lattices vs Crystal Groups

There is one more thing which confuses a lot of people: Bravais lattices vs crystal groups. It’s even possible that I made some mistakes with terminology in this article or elsewhere on the blog.

This is super confusing and not that important unless you need to describe complex crystal systems, so I’ll put it in collapsable text.

Click here to expand!

The term “crystal group” may also be called “crystal system” or “crystal family.” Basically, if you divided each of the space groups into an underlying Bravais lattice, you would find that some space groups could be both rhombohedral or hexagonal.

To avoid this, crystallographers invented a new term “crystal family” which combines rhombohedral and hexagonal into just the hexagonal crystal family. So, there are cubic, hexagonal, tetragonal, orthorhombic, monoclinic, and triclinic crystal families.

The term “crystal system” is used when crystallographers want to divide the hexagonal family into two: trigonal and hexagonal. The trigonal crystal system includes some point groups with rhombohedral and hexagonal underlying Bravais lattices.

Final Thoughts

In this article, you learned all about Bravais lattices! You learned about the Bravais lattices in 1D, 2D, and 3D.

The 3D Bravais lattices are important for categorizing crystals. Here is a summary table of the 14 Bravais lattices. You can click each one to view an entire article dedicated to that lattice and its related crystal structures.

Table: The 14 Bravais Lattices

3D Unit Cell Representation	Name	Vectors	Angles	Primitive Cell Representation	Space Groups	Unit Cell Volume	Examples
	Simple Cubic (SC)	a=b=c	α=β=γ=90°		195,198, 200,201,205, 207,208,212, 213,215,218, 221-224	a³	α-Polonium (α-Po), Cu₃Al, CsCl
	Face-Centered Cubic (FCC)	a=b=c	α=β=γ=90°		196,202,203, 209,210,216, 219,225-228	a³	Copper (Cu), Aluminum (Al), Nickel (Ni), NaCl, Diamond
	Body-Centered Cubic (BCC)	a=b=c	α=β=γ=90°		197,199,204, 206,211,214, 217,220,229, 230	a³	Tungsten (W), Lithium (Li), Vanadium (V), SiF₄
	Hexagonal	a=b≠c	α=120° β=γ=90°		143,144,145, 147,149,150, 151,152,153, 154,156,157, 158,159,162, 163,164,165	(3√3a²c)/2	Magnesium (Mg), Cobalt (Co), Rhenium (Re), BN, Graphite
	Rhombohedral	a=b=c	α=β=γ≠90°		146,148,155, 160,161,166, 167	a³√(1−3cos²α+2cos³α)	Mercury (Hg), β-Polonium (β-Po), α-Arsenic (α-As), α-Samarium (α-Sm) CuPt
	Simple Tetragonal	a=b≠c	α=β=γ=90°		75-78,81,83-86,89-96,99-106,111-118,123-138	a²c	CuAu, β-Neptunium (β-Np), CuTi₃
	Body-Centered Tetragonal	a=b≠c	α=β=γ=90°		79-80,82,87, 88,97,98,107- 110,119-122,139-142	a²c	Indium (In), Protactinium (Pa), β-Tin (β-Sn), Martensite
	Simple Orthorhombic	a≠b≠c	α=β=γ=90°		16-19,25-34, 47-62	abc	CdTe, AuCd
	Base-Centered Orthorhombic	a≠b≠c	α=β=γ=90°		20-21,35-41, 63-68	abc	α-Gallium (α-Ga), α-Uranium (α-U), Black Phosphorus (P), ZrSi₂
	Face-Centered Orthorhombic	a≠b≠c	α=β=γ=90°		22,42-43, 69-70	abc	γ-Plutonium (γ-Pu), TlF, α-Sulphur
	Body-Centered Orthorhombic	a≠b≠c	α=β=γ=90°		23-24,44-46, 71-74	abc	MoPt₂, ReSi₂, S₂Si
	Simple Monoclinic	a≠b≠c	α=β=90°≠γ		3-4,6-7, 10-11,13-14	abc sinγ	NiTi, high-pressure Tellurium (Te)
	Base-Centered Monoclinic	a≠b≠c	α=β=90°≠γ		5,8,9,12,15	abc sinγ	α-O₂, AuTe₂, CuO, β-Plutonium (β-Pu)
	Triclinic	a≠b≠c	α≠β≠γ≠90°		1-2	abc√(1−cos²α−cos²β− cos²γ+2cosαcosβcosγ)	PtI₄, FeS₂

References and Further Reading

You can check our figures for the unit cell volume here.

The examples of Bravais lattices were taken from this site.

Two great resources for crystals and crystal structures:

M. J. Mehl, D. Hicks, C. Toher, O. Levy, R. M. Hanson, G. L. W. Hart, and S. Curtarolo, The AFLOW Library of Crystallographic Prototypes: Part 1, Comp. Mat. Sci. 136, S1-S828 (2017). (doi=10.1016/j.commatsci.2017.01.017)
D. Hicks, M. J. Mehl, E. Gossett, C. Toher, O. Levy, R. M. Hanson, G. L. W. Hart, and S. Curtarolo, The AFLOW Library of Crystallographic Prototypes: Part 2, Comp. Mat. Sci. 161, S1-S1011 (2019). (doi=10.1016/j.commatsci.2018.10.043)

If you found this article helpful, odds are that you’re taking a class on structures. If you want to see the other crystallography-related articles I’ve written, here is this list, in recommended reading order:

Introduction to Bravais Lattices
What is the Difference Between “Crystal Structure” and “Bravais Lattice”
Atomic Packing Factor
How to Read Miller Indices
How to Read Hexagonal Miller-Bravais Indices
Close-Packed Crystals and Stacking Order
Interstitial Sites
Primitive Cells
How to Read Crystallography Notation
What are Point Groups
List of Point Groups
What are Space Groups
List of Space Groups
The 7 Crystal Systems

If you are interested in more details about any specific crystal structure, I have written individual articles about simple crystal structures which correspond to each of the 14 Bravais lattices:

1. Simple Cubic
2. Face-Centered Cubic
2a. Diamond Cubic
3. Body-Centered Cubic
4. Simple Hexagonal
4a. Hexagonal Close-Packed
4b. Double Hexagonal Close-Packed (La-type)
5. Rhombohedral
5a. Rhombohedral Close-Packed (Sm-type)
6. Simple Tetragonal
7. Body-Centered Tetragonal
7a. Diamond Tetragonal (White Tin)
8. Simple Orthorhombic
9. Base-Centered Orthorhombic
10. Face-Centered Orthorhombic
11. Body-Centered Orthorhombic
12. Simple Monoclinic
13. Base-Centered Monoclinic
14. Triclinic