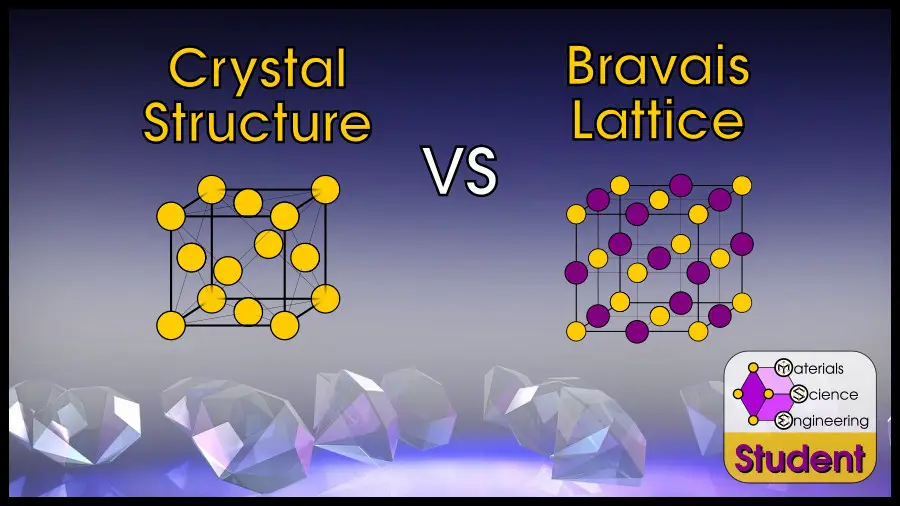
In many materials science classes, students will not distinguish between crystal structure and crystal lattice (more properly called “Bravais” lattice). To them, FCC just means “face-centered cubic” without considering whether they mean the FCC crystal structure or FCC Bravais lattice. You can even see this confusion even in Wikipedia articles, which cross between crystal structure and Bravais lattice even within the same table.
In crystallography, a Bravais lattice is one of 14 arrangements to fill space by translation. A crystal structure combines the lattice (how atoms are translated) with a basis (which atoms are translated) which theoretically describes every atom in the crystal. People often confuse “lattice” with “crystal” because the most common crystal structures have a basis of 1 atom, which looks exactly like the underlying Bravais lattice.
Outline
What Are Crystal Lattices?
I’ve previously written an in-depth article about Bravais lattices, which you can read here. That article explains a bit of the math, discusses the Bravais lattices in 1D, 2D, and 3D, and gives a full definition of each type of lattice.
Since you can read that any time you like, in this section I’ll give a shorter recap.
A Bravais lattice is a mathematical description that shows how space can tesselate infinitely by translation. (Tesselate means you can fill a space with a repeating pattern without gaps or overlaps. Translate means to slide, without rotating or inverting). For example, you can fill an infinite chessboard with squares. However, you couldn’t fill an infinite chessboard with identical triangles (unless you rotated some of them).
In 3 dimensions (i.e. the real world), there are 14 patterns to fill space by translation. The specifics aren’t important for this article; you should just know that any repeating, translated pattern can be categorized in one of these 14 Bravais lattices.
To make this categorization, you need to define a “lattice point” (when we get to crystal structures, you’ll see that “lattice point” and “basis” mean essentially the same thing).
You can then find the relationships between lattice points by drawing vectors (the length and direction between two points). All 3D Bravias lattices will have 3 vectors, and depending on the relationship between the vectors (such as if they are the same size, or the angle between them), a different Bravais lattice will be defined.
For example, the “simple cubic” Bravais lattice has 3 vectors which are the same length and are at 90º to each other (which forms a cube).
Unfortunately, Bravais lattices are a mathematical construction, so it’s not really possible to illustrate the point without using a crystal (this is one of the reasons people so often confuse crystals and lattices).
For example, take a look at this artwork I redrew from one of M.C. Escher’s paintings. Technically this is a 2D crystal.
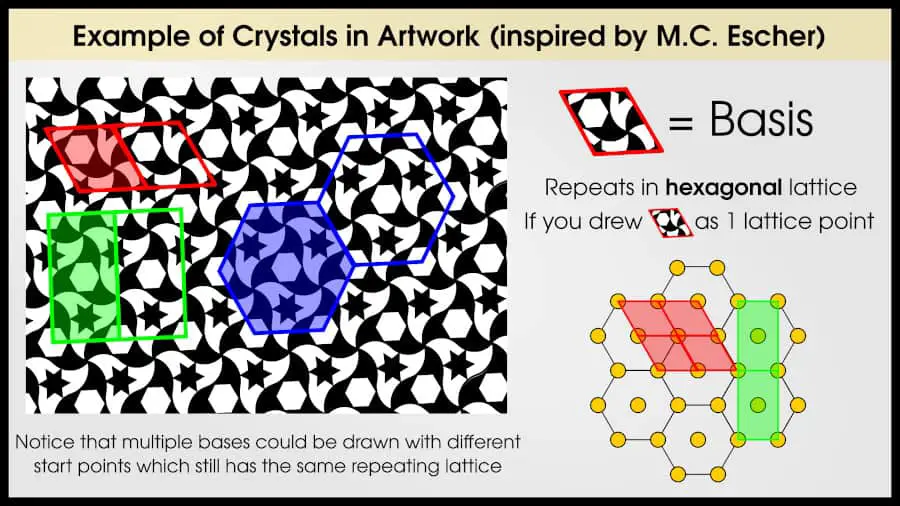
There is obviously a pattern here. Find some space which can be translated to tesselate. For example, I’ve outlined a rhombus in red. If I copied that red rhombus shape, I can break the entire picture into these rhombus shapes, where each one looks exactly the same. (Since we’re dealing with a real crystal, this rhombus shape is called a “basis” but I’ll get to that in the next section).
Now imagine that you have just the rhombuses. Distill each rhombus into a single point, at the rhombus center. Now, all you have are a series of points: lattice points.
You could compare this series of points with any list of 2D Bravais lattices, and you’d find that the lattice was “hexagonal.” If you drew vectors between lattice points, you’d see they form an angle of 120º, which is the definition for a hexagonal lattice. If you want a list of 2D and 3D Bravais lattices, you can find them in this article.
Now that you understand lattices, we can use them to build real crystals.
What Are Crystal Structures?
Crystals are a repeating unit in space. We typically consider them to be a repeating arrangement of atoms, but they can really be anything, even shapes in a painting (like my example inspired from M.C. Escher).
To make a crystal, you need a lattice and basis. The lattice is just a mathematical idea, but the basis is the “real” component which is repeated according to the mathematical lattice.
In the example with the M.C. Esher painting, each rhombus was actually a “basis.” Choosing a basis is mostly arbitrary–let’s return to the painting and see if we can identify any other bases.

Now, you can see that we could have chosen a different shape to tesselate the picture. However, regardless of the basis chosen, when you reduce it to a lattice, you end up with the same lattice!
In the same way, your choice of atomic basis can be arbitrary–as long as it forms a true repeating unit.
For example, let’s look at a 2D atomic arrangement with 2 types of atoms: yellow and green. At first glance, you may want to draw a square basis between 4 yellow atoms, with a green atom in the center. But if you try that, translating the square one unit over will NOT result in the same atomic configuration (the green atom is missing).
To compensate for this, you could expand your basis to 4x the area, so it includes 2 green atoms. Now, translating 1 unit over repeats exactly.
(Can you see that it is possible to make an even smaller basis? Hint: make the corners out of green atoms).
What Is the Unit Cell?
The unit cell is a small, repeating portion of the crystal. (Sometimes people say it’s the “smallest” repeating portion of the crystal, but that’s not true–see my article about primitive cells).
The unit cell shows the lattice and basis. For example, here is a diamond cubic unit cell:
This unit cell has an FCC Bravais lattice, but with a 2-atom basis.
Why Crystal Structure and Crystal Lattice Are Often Confused?
In the example I just gave you, it’s easy to tell the difference between the diamond cubic crystal, and the face-centered cubic lattice. But diamond cubic is not the most common crystal structure.
If I just said “FCC,” as so many materials scientists say–what does that mean? FCC is both a crystal structure, and a Bravais lattice. Specifically, the FCC crystal is when you have a 1-atom basis in the FCC lattice. As you just saw, diamond cubic is a 2-atom basis in the FCC lattice. There is another structure, the “rock salt” structure, which is has the FCC lattice but with 2 different atoms that form the basis.
Unless someone has updated the Wikipedia page since I wrote this article, samarium (Sm) seems to have a rhombohedral crystal structure. You would probably assume, then, that Sm atoms look like this:
This is the rhombohedral Bravais lattice. If you put one atom on each lattice point, you’d get the simple rhombohedral crystal structure. That is NOT how Sm actually looks. Sm is actually a close-packed structure like HCP–but with rhombohedral, rather than hexagonal symmetry.
In my opinion, calling this crystal structure “rhombohedral” is simply misleading. What Wikipedia should have said was that the Bravais lattice is rhombohedral. However, if the page only wrote lattices instead of real crystal structures, then other labels, such as HCP shouldn’t exist–there is no HCP lattice. HCP exists within the simple hexagonal lattice, but with a 2-atom basis. PeriodicTable.com actually does a better job of this because they only report Bravais lattice–however, the page title still says “ crystal structure.”
The Difference Between Lattice Point and Crystal Basis
In the course of this article, I may have confused you about the difference between lattice points and crystal bases. Let’s make sure we’re all clear here:
Lattice points are 0-dimensional points which identify the edges of a Bravais lattice. This may be confusing because, while the points are actually 0-dimensional they are often drawn as 2-dimensional circles.
Crystal bases are the set of atoms repeated along a Bravais lattice. Atoms are 3-dimensional, but are often drawn as 2-dimensional spheres. In common crystal structures such as FCC, HCP, and BCC, the crystal basis is just a single atom–so 1 atom = 1 basis = 1 lattice point. In more complex structures, such as diamond cubic or rock salt, you may see multiple atoms per basis.
There will always be 1 basis per lattice point–the difference is semantic, because a basis involves real space with real atoms, while a lattice point is a mathematical construct which imagines the space collapsed into a single point.
Final Thoughts
I hope this was a full explanation of the difference between crystal structures and crystal lattices. The difference is subtle, but many people confuse them. I tried to be as thorough as possible in this article to avoid confusion and to stop the propagation of misinformation, and I’m sorry if that made this article more difficult to read than most.
References and Further Reading
If you found this article helpful, odds are that you’re taking a class on structures. If you want to see the other crystallography-related articles I’ve written, here is this list, in recommended reading order:
Introduction to Bravais Lattices
What is the Difference Between “Crystal Structure” and “Bravais Lattice”
Atomic Packing Factor
How to Read Miller Indices
How to Read Hexagonal Miller-Bravais Indices
Close-Packed Crystals and Stacking Order
Interstitial Sites
Primitive Cells
How to Read Crystallography Notation
What are Point Groups
List of Point Groups
What are Space Groups
List of Space Groups
The 7 Crystal Systems
If you are interested in more details about any specific crystal structure, I have written individual articles about simple crystal structures which correspond to each of the 14 Bravais lattices:
1. Simple Cubic
2. Face-Centered Cubic
2a. Diamond Cubic
3. Body-Centered Cubic
4. Simple Hexagonal
4a. Hexagonal Close-Packed
4b. Double Hexagonal Close-Packed (La-type)
5. Rhombohedral
5a. Rhombohedral Close-Packed (Sm-type)
6. Simple Tetragonal
7. Body-Centered Tetragonal
7a. Diamond Tetragonal (White Tin)
8. Simple Orthorhombic
9. Base-Centered Orthorhombic
10. Face-Centered Orthorhombic
11. Body-Centered Orthorhombic
12. Simple Monoclinic
13. Base-Centered Monoclinic
14. Triclinic