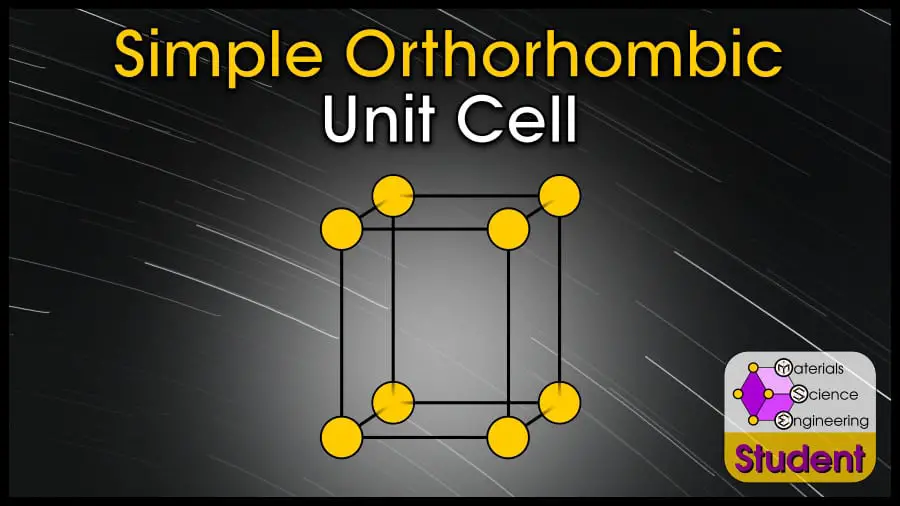
Simple Orthorhombic Unit Cell – Materials Science & Engineering

The orthorhombic unit cell looks like a box with 3 different edge lengths.

Since simple orthorhombic is one of the less-common crystal structures, I’m assuming someone searching for this is a somewhat advanced student in materials science, so I’ll give you the facts quickly and with little explanation. If you are new to materials science and don’t know what something means, you can check out my articles on the FCC, BCC, or HCP crystals, which explain terminology more slowly.

Although there are many crystal structures that fit with “orthorhombic” symmetry, the simple orthorhombic crystal structure (abbreviated SO in this article) has exactly 1 atom per lattice point in the simple orthorhombic Bravais lattice.

As far as I know, there are no real-world materials that exhibit a simple orthorhombic unit cell. If this structure were to exist, it would be a box with 3 different side lengths, with an atom on each corner. There are “primitive orthorhombic” crystals based on the Bravais lattice, which exist with multiple atoms that overall displays primitive orthorhombic symmetry. The simple orthorhombic unit cell would belong to space group #47 or Pmmm, with Pearson symbol oP1. There is no prototype or Strukturbericht for simple orthorhombic, since it does not exist with real atoms.

The simple orthorhombic unit cell can be imagined as a box with 3 different side lengths, with an atom on each corner. Pure materials never take this crystal structure, and it exists only mathematically. Simple orthorhombic has 1 atom per unit cell, lattice constants a, b, c, and 90º angles between vectors, Coordination Number CN = 2, and Atomic Packing Factor $APF=\frac{4 \pi r^3}{3abc}$ .

Outline

Common Examples of Simple Orthorhombic Materials
Simple Orthorhombic Coordination Number
Simple Orthorhombic Lattice Constants
Simple Orthorhombic Atomic Packing Factor
Final Thoughts
References and Further Reading

Common Examples of Simple Orthorhombic Materials

None.

However, there are still materials made of multiple kinds of atoms that have a primitive orthorhombic Bravais lattice, such as CdTe or Fe₃C.

Simple Orthorhombic Coordination Number

You can think of simple orthorhombic as a distortion of the simple cubic crystal. Simple cubic has 6-fold coordination, but if you changed the side lengths of two dimensions, you’d only have 2 nearest neighbors.

Simple orthorhombic has 2 nearest neighbors, but if the orthorhombic distortion is small you could imagine that there are 6 neighbors of nearly the same distance. However, there are no real materials that take this crystal structure.

Simple Orthorhombic Lattice Constants

The orthorhombic lattice is like a cube, where all sides are at 90º to each other, but with edge lengths distorted so there are three different edge lengths. Thus, the simple orthorhombic crystal has 3 lattice parameters: a, b, and c, which have an angle of 90º to each other

If we try to stay within the hard sphere model, we see that the close packed direction would be along the shorter edge.

Presumably, this shortest lattice parameter would have a length of $2r$ because atoms touch along this side, and the other two lattice parameters would have a length greater than $2r$ . However, there would be no physical reason to have three lattice parameters of different length, which is why the simple orthorhombic structure does not exist in real crystals.

If you wanted to describe the simple orthorhombic crystal with math, you would describe the cell with the vectors.

$\vec{a_1}=a\hat{x}$
$\vec{a_2}=b\hat{y}$
$\vec{a_3}=c\hat{z}$

Simple Orthorhombic Atomic Packing Factor

There is no simple answer for the simple orthorhombic APF, because the answer changes depending on the side lengths.

The volume of an orthorhombic unit cell is $abc$ , obtained by multiplying the lattice parameters times each other.

There is 1 atom split between each of the 8 corners of the cell, and nothing in the center, so the total is one full atom with a spherical radius of $\frac{4}{3} \pi r^3$ .

This allows us to write the theoretical APF in terms of the atomic radius and lattice constants.

$APF=\frac{\frac{4}{3} \pi r^3}{abc}=\frac{4 \pi r^3}{3abc}$

Final Thoughts

The simple orthorhombic crystal system does NOT exist in real life, and only arises by mathematical definition. There are many crystals which have an orthorhombic Bravais lattice, but these crystals have a more complicated “basis” which leads to asymmetrical lattice parameters.

References and Further Reading

If you want to know more about the basics of crystallography, check out this article.

If you weren’t sure about the difference between crystal structure and Bravais lattice, check out this article.

I also mentioned atomic packing factor (APF) earlier in this article. This is an important concept in your introductory materials science class, so if you want a full explanation of APF, check out this page.

If you’re interested in advanced crystallography or crystallography databases, you may want to check out the AFLOW crystallographic library.

For a great reference for all crystal structures, check out “The AFLOW Library of Crystallographic Prototypes.”

Single-Element Crystal Structures and the 14 Bravais Lattices

If you want to learn about specific crystal structures, here is a list of my articles about Bravais lattices and some related crystal structures for pure elements. Simple Orthorhombic is one of these 14 Bravais lattices and also occurs as a crystal structure.

1. Simple Cubic
2. Face-Centered Cubic
2a. Diamond Cubic
3. Body-Centered Cubic
4. Simple Hexagonal
4a. Hexagonal Close-Packed
4b. Double Hexagonal Close-Packed (La-type)
5. Rhombohedral
5a. Rhombohedral Close-Packed (Sm-type)
6. Simple Tetragonal
7. Body-Centered Tetragonal
7a. Diamond Tetragonal (White Tin)
8. Simple Orthorhombic
9. Base-Centered Orthorhombic
10. Face-Centered Orthorhombic
11. Body-Centered Orthorhombic
12. Simple Monoclinic
13. Base-Centered Monoclinic
14. Triclinic

Other articles in my crystallography series include:

Introduction to Bravais Lattices
What is the Difference Between “Crystal Structure” and “Bravais Lattice”
Atomic Packing Factor
How to Read Miller Indices
How to Read Hexagonal Miller-Bravais Indices
Close-Packed Crystals and Stacking Order
Interstitial Sites
Primitive Cells
How to Read Crystallography Notation
What are Point Groups
List of Point Groups
What are Space Groups
List of Space Groups
The 7 Crystal Systems