Diamond Tetragonal Unit Cell (White Tin) – Materials Science & Engineering

Diamond tetragonal (abbreviated DT in this article) is more commonly known as the β-Sn, or white tin crystal structure. It is one of the advanced crystal structures (because it doesn’t correlate 1-1 to a Bravais lattice), so if you’re searching for information about it, I’m assuming you’re a somewhat advanced student in materials science. I’ll give you the facts quickly and with little explanation. If you are new to materials science and don’t know what something means, you can check out my articles on the FCC, BCC, or HCP crystals, which explain terminology more slowly.

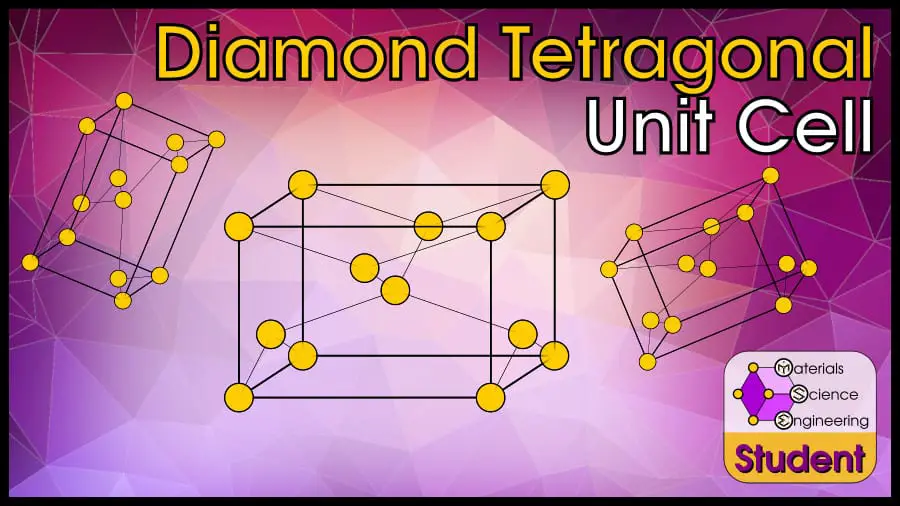
The Diamond Tetragonal (DT) unit cell can be imagined as a tetragon with an atom on each corner (0,0,0), the very center (½, ½, ½), and the non-square faces (½, 0, ¾) and (0, ½, ¼). DT has 8 atoms per unit cell, lattice constant a and c, Coordination Number CN = 4, and Atomic Packing Factor APF = 47%.

The diamond cubic crystal structure is based on the body-centered tetragonal Bravais lattice (remember that face-centered tetragonal is the same as body-centered tetragonal). There are 4 atoms per unit cell, and each atom is tetrahedrally coordinated so that it has 4 nearest neighbors. This crystal structure is similar to the diamond cubic crystal structure, but with a tetragonal distortion. The diamond tetragonal cell belongs to space group 141 or I4₁/amd, Strukturbericht A5, and Pearson symbol tI4. β-Sn is the prototype for DT.

Outline

Common Examples of Diamond Tetragonal Materials
Diamond Tetragonal Coordination Number
Diamond Tetragonal Lattice Constants
Diamond Tetragonal Atomic Packing Factor
Final Thoughts
References and Further Reading

Common Examples of Diamond Tetragonal Materials

The most famous material with the diamond tetragonal crystal structure is β-Sn, or white tin. In fact, the diamond tetragonal crystal structure is usually just called the white tin crystal structure. I prefer this name, however, because it more clearly identifies the atom positions.

As far as I know, white tin is the only element with the diamond tetragonal crystal structure at room temperature. However, both silicon and germanium can have the β-Sn crystal structure at non-STP conditions.

Diamond Tetragonal Coordination Number

The diamond tetragonal crystal structure is based on the diamond cubic crystal structure, but with a distortion along one axis. In diamond tetragonal, the atoms will maintain their 4-atom bonds, for a coordination number (CN) of 4. There are also 2 next-nearest neighbors.

Diamond Tetragonal Lattice Constants

Since a tetragon has three vectors at 90º to each other, where 2 are the same length and one is different, there are two lattice constants: a, b (which is also a), and c.

By convention, crystallographers use a and the c/a ratio to model most crystals that have two parameters: a and the c/a ratio.

If the c/a ratio is exactly $\sqrt{2}$ , then the crystal structure becomes diamond cubic. For tin, however, the c/a ratio is smaller than this, so the tetragon is squashed in the c-direction.

There is no geometric ratio that can be used to calculate the ideal lattice constant as a function of atomic radius. Such a ratio does exist for diamond cubic, so if the c/a ratio is exactly $\sqrt{2}$ , then a will be $\frac{8}{\sqrt{3}}r$ .

For white tin, the lattice parameters are $a=5.8312Å$ and $c=3.1814\r{A}$ [1].

If you wanted to describe the body-centered tetragonal crystal with math, you would describe the cell with the vectors

$\vec{a}_{1}=-\frac{a}{2}\hat{x}+\frac{a}{2}\hat{y}+\frac{c}{2}\hat{z}$
$\vec{a}_{2}=\frac{a}{2}\hat{x}-\frac{a}{2}\hat{y}+\frac{c}{2}\hat{z}$
$\vec{a}_{3}=\frac{a}{2}\hat{x}+\frac{a}{2}\hat{y}-\frac{c}{2}\hat{z}$

And the basis is

$B_{1}=\frac{7}{8}\vec{a}_1+\frac{1}{8}\vec{a}_2}+\frac{3}{4}\vec{a}_3}=\frac{3}{4}a\hat{y}+\frac{1}{8}c\hat{z}$
$B_{2}=\frac{1}{8}\vec{a}_1}+\frac{7}{8}\vec{a}_2}+\frac{1}{4}\vec{a}_3}=\frac{1}{2}a\hat{x}+\frac{3}{4}a\hat{y}+\frac{3}{8}c\hat{z}$

Diamond Tetragonal Atomic Packing Factor

For the diamond tetragonal crystal structure, there is no pretty way to write the lattice parameter as a function of atomic radius, so there is no “definite” APF value.

However, if you know your atomic radius and lattice parameters, you can calculate APF the same way as usual.

APF is the volume of space taken up by atoms, divided by the total volume of the unit cell.

The diamond tetragonal unit cell contains 4 atoms ( $8\cdot\frac{1}{8}$ on each corner, ( $4\cdot\frac{1}{2}$ on each face, and 1 full atom in the center).

Using the hard sphere model, the volume of each atom is $\frac{4}{3}\pi r^3$ , and the volume of a tetragon is $a^2c$ .

Thus, $APF =\frac{4\cdot\frac{4}{3}\pi r^3}{a^2c}=\frac{16\pi r^3}{3a^2c}$

For white tin, which has lattice parameters $a=5.8312\r{A}$ and $c=3.1814\r{A}$ , and $radius=1.45\r{A}$ [2], the atomic packing factor is 0.47.

Final Thoughts

The white tin crystal structure is a tetragonally distorted version of the diamond cubic crystal structure. This packing factor is actually higher than the diamond cubic packing of gray tin, which is why the transformation from white tin to gray tin results in a volume expansion that rips the solid material into a powder.

References and Further Reading

If you want to know more about the basics of crystallography, check out this article about crystals and grains.

If you weren’t sure about the difference between crystal structure and Bravais lattice, check out this article.

I also mentioned atomic packing factor (APF) earlier in this article. This is an important concept in your introductory materials science class, so if you want a full explanation of APF, check out this page.

If you’re interested in advanced crystallography or crystallography databases, you may want to check out the AFLOW crystallographic library.

For a great reference for all crystal structures, check out “The AFLOW Library of Crystallographic Prototypes.”

[1] V. T. Deshpande and D. B. Sirdeshmukh. Thermal Expansion of Tetragonal Tin. Physics Department, College of Science, Osmania University, Hyderabad – 7, India, Acta Cryst. (1961). 14, 355. https://doi.org/10.1107/S0365110X61001212

[2] J. C. Slater, Atomic Radii in Crystals, J. Chem. Phys. 41, 3199 (1964); https://doi.org/10.1063/1.1725697

The 14 Basic Crystal Structures

If you want to learn about specific crystal structures, here is a list of my articles about Bravais lattices and some related crystal structures for pure elements.

1. Simple Cubic
2. Face-Centered Cubic
2a. Diamond Cubic
3. Body-Centered Cubic
4. Simple Hexagonal
4a. Hexagonal Close-Packed
4b. Double Hexagonal Close-Packed (La-type)
5. Rhombohedral
5a. Rhombohedral Close-Packed (Sm-type)
6. Simple Tetragonal
7. Body-Centered Tetragonal
7a. Diamond Tetragonal (White Tin)
8. Simple Orthorhombic
9. Base-Centered Orthorhombic
10. Face-Centered Orthorhombic
11. Body-Centered Orthorhombic
12. Simple Monoclinic
13. Base-Centered Monoclinic
14. Triclinic

Other articles in my crystallography series include:

Introduction to Bravais Lattices
What is the Difference Between “Crystal Structure” and “Bravais Lattice”
Atomic Packing Factor
How to Read Miller Indices
How to Read Hexagonal Miller-Bravais Indices
Close-Packed Crystals and Stacking Order
Interstitial Sites
Primitive Cells
How to Read Crystallography Notation
What are Point Groups
List of Point Groups
What are Space Groups
List of Space Groups
The 7 Crystal Systems