
Most mechanical properties relate to deformation in some way. Since deformation is the way a material moves in response to a force, force and displacement will be essential in defining most mechanical properties.
However, force and displacement are extrinsic properties. That means they are related to the amount of material you have. A building can withstand much more force than a spoon simply because the building is bigger. Similarly, the building may sway several centimeters in the wind, while a spoon will experience unnoticeable displacement in the strongest gale.
But if they are made of the same material, the material should have constant mechanical properties. These intrinsic corollaries to force and displacement is stress and strain.
Stress is the force per cross-sectional area that a material withstands. Strain is the percent change in the length of the material. The stress-strain curve is the simplest way to describe the mechanical properties of the material. The stress-strain curve can provide information about a material’s strength, toughness, stiffness, ductility, and more.
Outline
Introduction to Stress and Strain in a Tensile Test
To transform extrinsic force and displacement into intrinsic stress and strain, we need to divide by the amount of material.
The most basic test of a material’s mechanical properties is a tensile test. In a tensile test, the material is shaped uniformly and pulled.
Since force acts over a cross-sectional area, we define stress as the force per unit area.
where is the stress,
is the applied force, and
is the cross-sectional area.
In other words, stress is the same as pressure.
Similarly, we define strain as the percent change in length. The total displacement is the change in length, so strain is the change in length divided by the original length.
where is the strain,
is the change in length, and
is the length.
| Extrinsic Properties | Intrinsic Properties | ||
|---|---|---|---|
| Force | Displacement | Stress | Strain |
Now that we have force and displacement, we can measure samples of many different shapes. The building deforms more than a spoon when the wind blows, but that’s because 0.1% of a 100 meter building is 10 centimeters, but 0.1% of a 10 centimeter spoon is 0.1 mm.
If you’ve been paying attention, you may have noticed a flaw in my equations. It’s true, I’ve simplified.
The problem is that when you pull your sample, the length increases, but the cross-sectional area decreases. What I showed you doesn’t account for the sample changing size.
Most engineers would prefer to ignore the changing sample size. To do this, they simply divide by the sample’s original dimensions instead of the constantly changing dimensions. All I have to do is add some subscript “0s” to specify that these are the original dimensions, and now I have
Engineering Stress:
And Engineering Strain:
In contrast, true stress uses the instantaneous cross-sectional area, so is the current cross-sectional area, which is continually changing.
True Stress:
True Strain:
If you want the full math, remember that you can expand text in the hidden sections. If you don’t want to expand it, the math details will be hidden from you and you can continue reading about why true stress and true strain don’t matter as much as engineering stress and strain.
Click here to see the math.
If you’re seeing this, congratulations for being adventurous enough to look at the math!
Instead of using which represents large changes, I use a derivative, which indicates infinitesimal changes. Thus,
becomes
and integrating between the original values and current (instantaneous) values,
Solving the integral, and remembering that
simplifying
As I mentioned, engineers prefer the much simpler calculations from engineering stress and strain. If you want to know more about true stress and strain, (probably because you need help on that homework problem), you can check out this article.
Otherwise, on this article and elsewhere on the site, if I say “stress” or “strain”, you can assume I mean engineering stress and engineering strain.
The Stress-Strain Curve
Stress and strain can be related in several different ways. For example, if you wanted to measure how a material survives a bullet, stress is the force-per-area of the bullet, and strain is how much the material moves.
You could also look at how stress and strain are affected by changing temperatures or long times (creep), or how they change if you repeat the stress many times (fatigue).
The stress could be applied in tension, compression, or shear.
But when engineers say “the stress-strain curve,” they mean a graph that results from a simple tensile test. A material is pulled and a machine measures the changing length and force.
You can think of this graph as having “force” on the y-axis, and changing length on the x-axis. I know the y-axis is labelled as “stress,” but remember that–since this is engineering stress–the only thing changing is the force. The y-axis is the pulling force divided by the sample’s initial area.
When I first saw this chart, I thought the x-axis and y-axis should be reversed. Shouldn’t the force be the independent variable, which causes a length change?
It could be, but as engineers it’s actually easier to measure the opposite way.
Standard tensile tests pull the sample at a certain rate. For example, it might move 1 millimeter per minute. Then it measures how much force was required to make the movement. The machine applies a strain and measures the stress.
That’s why strain is on the x-axis, and stress is on the y-axis.
The standard stress-strain curve is obtained by this tensile test at room temperature and a constant strain rate.
“Regimes” of the Stress-Strain Curve
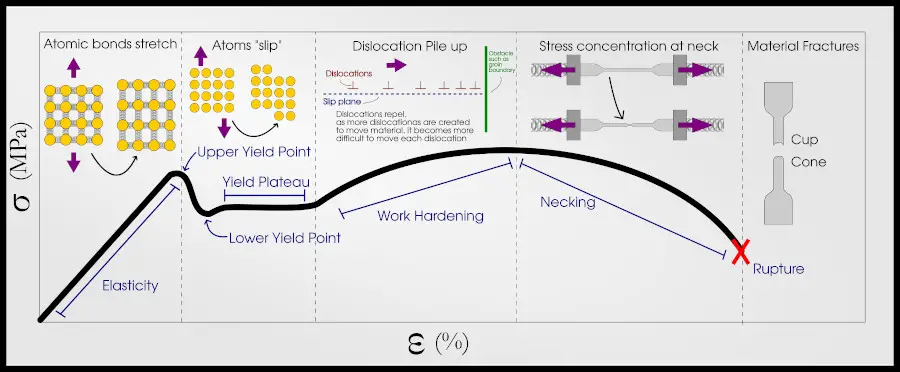
When the material is first exposed to force, it behaves elastically. Elastic behavior means that however the material moves while under load, it returns to its original position when the load is removed. This happens because the atomic bonds are stretching, so elastic behavior occurs in every material (although sometimes the elastic regime might be really small).
The slope of this line relates to a property called “stiffness.” In this most basic case, the slope provides “Young’s Modulus.”
Stiffness is crucial to engineers because most real-life applications involve materials in the elastic regime.
Remember, as long as your material stays in the elastic regime, it will suffer zero permanent deformation (according to this model). That makes engineers happy because it’s an easy way to guarantee safety.
Remember, as long as your material stays in the elastic regime, it will suffer zero permanent deformation (according to this model).
That makes engineers happy because it’s an easy way to guarantee safety.
Think of a paperclip. If you bend it just a little, it will bounce back every time. This is the elastic region. If you bend it far, however, you will permanently bend the clip.
At a certain stress, the material will leave the elastic region. This stress is called the “yield strength.”
At any point past the yield strength, the material will suffer permanent deformation.
Once the material yields, it enters the “plastic” regime. (Polymer plastics are named so because they have a very large plastic regime).
In the plastic regime, atomic bonds are broken and reformed. Surprisingly, the material strength increases during this time because of dislocation pile-up.
I will explain the specifics in another article, but I’m sure you know this intuitively. When you bend a paperclip, at first, bending the clip makes it stronger. This is the same phenomenon.
Strain hardening, or work hardening, will continue until the material breaks.
But remember: as we pull the material, the cross-sectional area decreases. Since this is an engineering stress-strain curve and we assume the cross-sectional area stays the same, the stress appears to decrease.
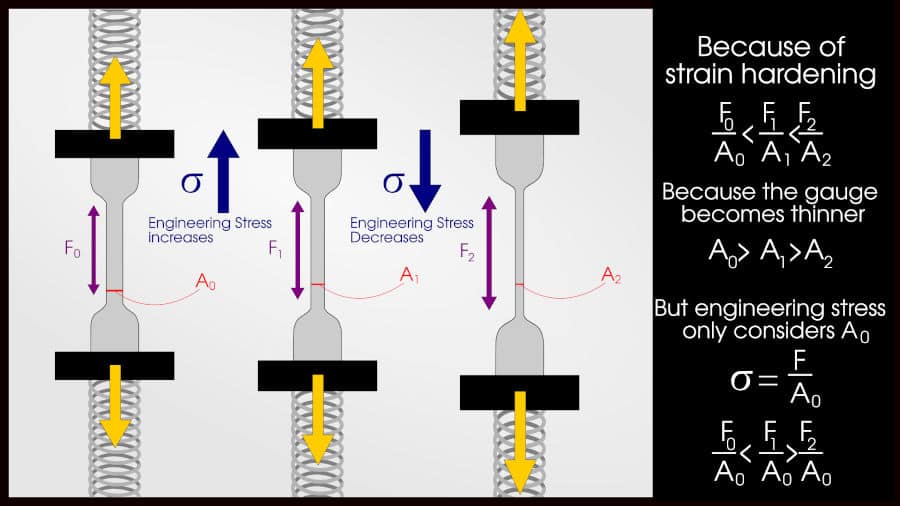
The effect becomes even more pronounced when the material starts to “neck.” Necking is when one part of the sample becomes a little bit thinner than the rest. Then, all of the stress is concentrated in this thin part.
The strength increase due to work hardening must compete with the strength decrease due to necking.
The maximum value of stress on an engineering stress-strain curve is called the “ultimate tensile strength.” That is the highest load the sample could possibly bear.
In the tensile test, because we control the strain, we can continue to stretch the material and see the point at where it breaks. This is the fracture strain.
In a real situation, where some part of a bridge experiences forces, once the bridge reaches the ultimate strength, since the forces are now higher than the strength, the material will immediately stretch to the fracture strain and fail catastrophically.
Of course, real materials will never be subjected to forces close to the ultimate tensile strength. For practical purposes, the yield strength is considered the upper bound for engineers.
The Stress-Strain Curve for Metals, Ceramics, and Polymers
The curve I have shown you is a typical curve for ductile materials.
Plasticity happens when the atoms “slip”–when they break bonds and reform new ones. Metallic bonding is great for this sort of re-bonding, which is why metals are usually ductile.
The stress-strain curve you have seen so far is typical of metals.
This is another curve, typical of metals (especially steel). In this case, the slip happens over a relatively wide strain range before dislocation pileup causes strain hardening. There is also a slight decrease after the initial yield, leading to an upper yield point and lower yield point.
Ceramics tend to have much higher yield strengths, but because they are so brittle, their yield strength, ultimate strength, and fracture strength are the same.
Polymers can have many different stress-strain behaviors, especially because certain polymer interactions can change at different stress levels, but they will generally be less strong, but more ductile, than metals.
Here is a sketch of stress-strain curves for metals, ceramics, and polymers on one graph.
Note that ceramics are typically the strongest, polymers have the greatest elongation, and metals are often the toughest.
Review! What Does the Stress-Strain Curve Say about a Material?
Throughout this article, I’ve explained certain terms that relate to the stress-strain curve.
Now, let’s revisit those terms, and some new ones, to see all the different properties a stress-strain curve can tell us about material.
But before we dive in, let’s have a look at the stress-strain curve and see what happens with the stretched material at every stage!
What is Elastic Modulus?
Elastic Modulus is the slope (stress divided by strain) of the elastic region. In a tensile test, this is Young’s Modulus (shear modulus and bulk modulus also exist).
What is Proportional Limit?
Proportional Limit is the straight-line portion of the elastic regime. This is often the same as the yield point, but in exceptionally clean graphs, it may be possible to distinguish between the two points.
What is Yield Strength?
Yield Strength (or yield stress, or yield strain) is the point between the elastic region and the plastic region. This can sometimes be hard to determine, so it is conventionally defined as having 0.2% plastic deformation. You can find this point by drawing a line of Young’s modulus starting at 0.002 strain, and finding where it intersects with the stress-strain curve.
What is Plastic Deformation?
Plastic Deformation is the permanent deformation the material has. In the elastic regime, there is no permanent deformation. Past the yield stress, permanent deformation is the current strain minus the yield strain.
What is Ultimate Strength?
Ultimate Strength, or in this case, ultimate tensile strength (UTS) is the highest engineering stress the material can endure. In an engineering stress-strain curve, this is the maximum point. It marks the point where necking overtakes strain hardening.
What is Strain Hardening?
Strain Hardening is when materials get stronger as they deform. This effect is caused by dislocation interaction. Strain hardening is the reason that the stress-strain curve increases past the yield stress. If there was no strain hardening, stress would flatline at the yield stress until necking occured.
What is Necking?
Necking is when one region of the gauge becomes thinner than the rest. At first, as the material elongates, the cross-sectional area will uniformly reduce. At some point, one section of the area becomes just a bit thinner than the rest. This concentrates the stress, essentially creating a new tensile test with a smaller gauge diameter.
What is Fracture Stress?
Fracture Stress, or failure stress, or rupture stress, is the stress at which the tensile specimen breaks. Fracture stress is generally meaningless in an engineering stress-strain curve, because it is below the ultimate tensile strength. Fracture strain may be significant, because it indicates how much the material has stretched when it finally breaks. In a true stress-strain curve, fracture stress can be meaningful because it indicates the maximum strength of the strain-hardened material.
What is Elongation?
Elongation is the change in length of the tensile gauge. This is generally equivalent to the fracture strain (or final strain, if the material does not break). The degree of elongation can indicate how ductile a material is.
What is Ductility?
Ductility refers to how much plastic deformation a material can survive. Materials with high fracture strains are considered very ductile; materials with fracture strains near the yield strain are brittle.
What is Toughness?
Toughness is the amount of energy a material can absorb. That means work, or force*distance. Conveniently, the stress strain curve essentially plots force on the y-axis and distance on the x-axis, so toughness is the area under the stress-strain curve. There are several kinds of toughness (like fracture toughness or notch toughness). Taking the area under the stress strain curve is a generic way to measure low strain rate toughness.
What is Resilience?
Resilience is a material’s recoverable energy from elastic deformation. It’s basically toughness but only for the elastic portion of the graph.
Modulus of Resilience:
where is the modulus of resilience,
is the yield strain, and
is the stress.
Resilience is good for storing elastic energy. Springs should be made from a material with a high modulus of resilience.
Assuming this area is a right triangle (which introduces slight error), then
so highly resilient materials need a high yield strength and low elastic modulus.
Final Thoughts
Now, you know (almost) everything about the stress-strain curve in materials science! I skipped some advanced details about true stress and true strain, so if you’re interested in that, check out this article.
This article was part of a series about mechanical properties.
