Simple Rhombohedral Unit Cell – Materials Science & Engineering

Alright, now we’re getting to the less-common crystal structures. If you’re searching for information about rhombohedral crystal cells, I’m assuming you’re a somewhat advanced student in materials science, so I’ll give you the facts quickly and with little explanation. If you are new to materials science and don’t know what something means, you can check out my articles on the FCC, BCC, or HCP crystals, which explain terminology more slowly.

A “rhombohedral” crystal structure is any that fits into a rhombohedral Bravais lattice, or in space groups #146, 148, 155, 160, 161, 166, or 167. However, this article will focus on the “simple” or “primitive” rhombohedral unit cell, which has a single atom at each lattice point on a rhombohedron, abbreviated as SR for this article. The simple rhombohedral unit cell belongs to space group #166 or $R\bar{3}m$ , Strukturbericht A_i or A10 (depending on the rhombohedral angles), and Pearson symbol hR1. α-Hg (A10) or β-Po (A_i) are the prototypes for this crystal structure.

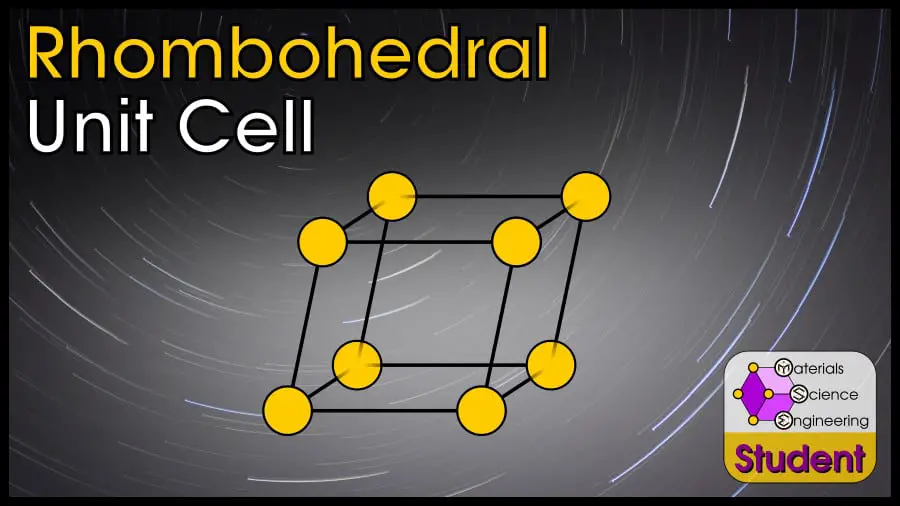
The Simple Rhombohedral (SR) unit cell can be imagined as a rhombohedron with an atom on each corner. It is an uncommon crystal structure. SR has 1 atom per unit cell, lattice constant a = 2r (or $a=\frac{r}{\sin{\frac{\alpha}{2}}}}$ ), Coordination Number CN = 6, and Atomic Packing Factor APF ranging from 0.52 to 0.74.

Simple rhombohedral is a rare crystal structure, but there are at least two materials that arrange in this manner.

Outline

Common Examples of Rhombohedral Materials
Rhombohedral Coordination Number
Rhombohedral Lattice Constants
Rhombohedral Atomic Packing Factor
Final Thoughts
References and Further Reading

Common Examples of Rhombohedral Materials

There are no elements that have a SR crystals structure at standard pressure and temperature. However, non-STP phases β-polonium and α-mercury do exhibit this crystal structure.

I also found one paper that found a SR phase in lithium–it was essentially the FCC phase, but with a 7% shrinkage along one of the body diagonals, and expansion in the other directions.

SR is rare because it is asymmetrical and has a low coordination number and low packing factor. That means it is not a very stable structure.

Some studies predict that SR exists in other phases in extreme environments, such as in sodium.

Rhombohedral Coordination Number

The simple rhombohedral can be thought of as a distortion of the simple cubic (SC) crystal.

Counting the nearest neighbors (NNs) is tricky, because there are many atoms with slightly different distances. For example, the β-polonium structure has 6 NN and 6 next-nearest neighbors (NNN).

Rhombohedral Lattice Constants

The rhombohedral lattice is like a cube, where you pull two opposite corners apart. Actually, you could consider the simple cubic (SC), face-centered cubic (FCC), and body-centered cubic (BCC) to be “subsets” of the rhombohedral cell with special symmetries. If you took α as the angle between two lattice vectors, α=90º is SC, α=60º is FCC, and α=109.47º is BCC.

This why crystallographers sometimes distinguish between the two types of simple rhombohedral crystal. β-polonium (with Strukturbericht A_i) is rhombohedral with an angle between that of BCC and SC, while α-mercury (with Strukturbericht A10) is rhombohedral with an angle between that of SC and FCC.

If we try to stay within the hard sphere model, we see that the close packed direction would either be along one edge, or along the face diagonal, depending on the angle α.

First, lets look at a rhombus and imagine that α was extremely small, so the lattice parameter $a$ is very large. You’ll see that the opposite-side atoms touch, while the left and right atoms can move infinitely far away. With some basic trigonometry, $a=\frac{r}{\sin{\frac{\alpha}{2}}}$ .

As we bring the left and right atoms closer to the center, at some point they will touch the top and bottom atoms. Now, the lattice parameter is exactly $2r$ . At this moment, α=60º and we actually have an FCC primitive unit cell.

If we try to increase the angle $\alpha$ further, by squeezing the left and right atoms even closer together, the lattice parameter will stay $2r$ because the atoms are modeled as hard spheres. Instead, the top and bottom atoms move further away. Once α=90º, by definition, this would be a simple cubic unit cell. (If you’re curious α=109.471º is BCC).

In summary, the lattice parameter $a$ depends on the angle between lattice vectors $\alpha$ . For $60^{\circ} \textdegree \le \alpha < 90^{\circ}, a=2r$ and for $\alpha < 60^{\circ}, a=\frac{r}{\sin{\frac{\alpha}{2}}}$ .

If you wanted to describe the simple rhombohedral crystal with math, you would describe the cell with the vectors

$\vec{a}_{1}=a(1+x)\hat{x}+a\hat{y}+a\hat{z}$
$\vec{a}_{2}=a\hat{x}+a(1+x)\hat{y}+a\hat{z}$
$\vec{a}_{3}=a\hat{x}+a\hat{y}+a(1+x)\hat{z}$

Where “x” relates the distortion away from cubic. If x=⅓, the crystal would be FCC. If x= 0, the crystal would be SC. If x=-1/6, the crystal would be BCC. If you used vector math to put “x” in terms of the angle between vectors, $\alpha$ , you’d see that x=⅓ corresponds to α=60º, x=0 corresponds to α=90º, and x=-1/6 corresponds to α=109.47º.

Rhombohedral Atomic Packing Factor

There is no simple answer for the simple rhombohedral APF, because the answer changes depending on the rhombohedral angle.

The volume of the rhombohedron is

$V=a^3\sqrt{1-3\cos^2\alpha+2\cos^3\alpha}$

There is 1 atom split between each of the 8 corners of the rhombohedron, and nothing in the center, so the total is one full atom with a spherical radius of $\frac{4}{3}\pi r^3$ .

$APF=\frac{\frac{4}{3}\pi r^3}{a^3\sqrt{1-3\cos^2\alpha+2\cos^3\alpha}}=\frac{4\pi r^3}{3a^3\sqrt{1-3\cos^2\alpha+2\cos^3\alpha}}$

We also know $a$ depends on the angle between lattice vectors $\alpha$ . For $60^{\circ} \textdegree \le \alpha < 90^{\circ}, a=2r$ and for $\alpha < 60^{\circ}, a=\frac{r}{\sin{\frac{\alpha}{2}}}$ which allows us to write the theoretical APF in terms of the rhombohedral angle and the atomic radius. Note, however, that low-symmetry structures like simple rhombohedral are a bit further from the hard sphere model, so this theoretical APF may not perfectly match the APF of real crystals.

Below is a Desmos graph that plots APF in terms of the vector angle α. You can see that α=60º results in an APF of 0.74, α=90º has an APF of 0.52, and α=109.47º has an APF of 0.68. If you don’t have those values memorized, you should go back and read my article about APF!

In summary, the APF for simple rhombohedral ranges from 0.52 to 0.74 (although, technically if α is below 60º and gets close to 0º, the unit cell would get infinitely large and APF would go to zero. That situation would never happen with real atoms, however)

Final Thoughts

The Simple Rhombohedral (SR), or primitive rhombohedral unit cell, is an unusual way that atoms can be arranged in solids. This crystal structure is found in non-STP phases of polonium, mercury, and lithium.

References and Further Reading

If you want to know more about the basics of crystallography, check out this article about crystals and grains.

If you weren’t sure about the difference between crystal structure and Bravais lattice, check out this article.

I also mentioned atomic packing factor (APF) earlier in this article. This is an important concept in your introductory materials science class, so if you want a full explanation of APF, check out this page.

If you’re interested in advanced crystallography or crystallography databases, you may want to check out the AFLOW crystallographic library.

For a great reference for all crystal structures, check out “The AFLOW Library of Crystallographic Prototypes.”

Single-Element Crystal Structures and the 14 Bravais Lattices

If you want to learn about specific crystal structures, here is a list of my articles about Bravais lattices and some related crystal structures for pure elements. Simple Rhombohedral is one of these 14 Bravais lattices and also occurs as a crystal structure.

1. Simple Cubic
2. Face-Centered Cubic
2a. Diamond Cubic
3. Body-Centered Cubic
4. Simple Hexagonal
4a. Hexagonal Close-Packed
4b. Double Hexagonal Close-Packed (La-type)
5. Rhombohedral
5a. Rhombohedral Close-Packed (Sm-type)
6. Simple Tetragonal
7. Body-Centered Tetragonal
7a. Diamond Tetragonal (White Tin)
8. Simple Orthorhombic
9. Base-Centered Orthorhombic
10. Face-Centered Orthorhombic
11. Body-Centered Orthorhombic
12. Simple Monoclinic
13. Base-Centered Monoclinic
14. Triclinic

Other articles in my crystallography series include:

Introduction to Bravais Lattices
What is the Difference Between “Crystal Structure” and “Bravais Lattice”
Atomic Packing Factor
How to Read Miller Indices
How to Read Hexagonal Miller-Bravais Indices
Close-Packed Crystals and Stacking Order
Interstitial Sites
Primitive Cells
How to Read Crystallography Notation
What are Point Groups
List of Point Groups
What are Space Groups
List of Space Groups
The 7 Crystal Systems