
Almost everything around you is a crystal. Most people think of crystals as some rare, precious gemstone like diamonds or rubies, but perhaps you know that salt, sugar, and ice are also crystals. What about steel, silicon, bricks, copper, or fingernails? Yep, those are crystals, too!
Modern humans use more polymers and glass than previous societies, but almost all other inorganic materials are crystalline.
Crystals are materials that have a repeating arrangement of atoms. Single crystals, like gemstones, have a single grain so the periodic array of atoms is never interrupted. Polycrystals, like metal, have many grains which are usually too small to see. Crystal structure is one of the most basic properties of a material.
While single crystals (like gemstones) may be rare, crystals in general are not. In this article, I’ll explain what crystals and grains are and why they are important.
Outline
Periodic Arrangement of Atoms
Boy, that sounds fancy. A periodic arrangement of atoms just means that the atoms repeat in some pattern. Usually, this pattern is super simple.
Think back to school, when you learned about solids, liquids, and gasses. You have a model for how a solid looks, right? Where are the atoms in a solid? I bet you imagined something like this:
What do you know, that’s a crystal! See how the atomic pattern repeats? Each atom touches another atom in the same direction. Although you can’t see all the atoms from this perspective, you could tell me exactly how many atoms are in the box. Furthermore, you could predict, right now, whether this spot with a question mark has an atom or an empty space.
Once you know the basic orientation and crystal pattern, you should be able to know where every other atom is. (You can’t actually do this in real life because of crystal defects, but I hope you understand my point.)
The opposite of a crystal–a solid which has its atoms arranged randomly–is called an amorphous solid. Glass is in amorphous solid.
There are also materials that are called “semi-crystalline,” like many polymers or composites. Semi-crystalline materials are not perfectly random, but they don’t line in perfect arrays either.
The Unit Cell: Lattice and Basis
When we talk about crystal structures, we define a unit cell. The unit cell is the basic repeating block of a crystal. To define a unit cell, we need to use a lattice and basis.
The lattice is the way that we define a repeated unit. The basis is the thing which is repeated. The lattice is how the thing is repeated.
Here is a simple, 2-dimensional square lattice.
The lattice is a square with side length a, which repeats at a distance a, at 90 degrees. The repeated unit, or basis, is a single circle. You could define this basis by looking at the 4 quarters of different circles, or by putting the basis in the center of the lattice as one full circle. Either way, the lattice is a square of a2, with 1 circle per lattice.
Notice that it’s also possible to define a larger lattice and basis. If you looked at some arbitrary rectangle with dimensions , with 6 circles contained within (count the fractions:
), you would be describing the same structure. The lattice would have an area of
, with 6 atoms inside.
While this larger lattice and basis would accurately describe the crystal, the simpler version is considered to be better.
Let’s look at a slightly more complicated crystal.
Now, you see there is a green circle in between some of the yellow circles. If there were a green circle between every 4 yellow circles, we could define the basis as before.
However, if we just defined the unit cell as before, you’ll see that it doesn’t repeat.
Instead, we need a larger unit cell. This one fully captures the symmetry and repeats exactly. Now you know that we have a valid lattice and basis.
If we use the smallest unit cell possible, there are only a certain number of fundamental lattice patterns. These are called Bravais Lattices (pronounced like Bra-Vay). In 2 dimensions, there are 5 Bravais lattices. In 3 dimensions, there are 14 Bravais lattices.
If you are interested in crystallography I’d recommend checking out this article about the 14 Bravais lattices. In this article, I’ll just focus on the 4 crystal structures you’ll likely see in a materials science class.
Common Crystal Structures
If you look at the crystal structures of each element, you’ll notice that some structures are especially common.
The three most common structures are face-centered cubic (FCC), body-centered cubic (BCC), and hexagonal close-packed (HCP). I’ll also talk about simple cubic (SC) because it’s easy to explain, although it’s not a common structure.
In other articles, I also have a full breakdown of each crystal structure.
Simple Cubic (SC)
The simple cubic unit cell is just a cube with an atom on each corner. In total, there is 1 atom per unit cell. If you want to know more about simple cubic crystal structure, here you’ll find a detailed explanation.
The side length of each cube, , is just
because the atoms touch along the sides. If you calculated the APF, you’ll find that SC has 52% packing density. That means it’s half empty space!
As you can imagine, SC is not a very stable crystal structure, so it’s pretty rare.
Face-Centered Cubic (FCC)
Face-Centered Cubic is also called “cubic close-packed” (CCP) in older textbooks, because it is the closest-packed cubic arrangement of atoms. Click here if you want more information on FCC.
FCC is a cube with an atom on each corner, and another on each face. There are 4 atoms per unit cell.
If you calculated it, you’d see that the side length and the APF=74%. That is the highest-packing possible for a crystal made of a single atom, which is why FCC is so common for pure materials.
Body-Centered Cubic (BCC)
Body-Centered Cubic is the 3rd kind of cubic structure. This is nearly close-packed.
BCC can be imagined as a cube with an atom on each corner, and another atom in the center. There are 2 atoms per unit cell in BCC. For more on BCC, check out this post.
Again, all the math can be found in this article, but if you work through it you’ll see that BCC unit cell has a side length and APF of 68%.
68% is not as good as 74%, but it’s close enough to be very common.
Although FCC and BCC are both cubic, they actually have a ton of differences. That’s a bit more advanced to talk about in this article, but you can see the differences between FCC and BCC in this article.
Hexagonal Close-Packed (HCP)
Hexagonal Close-Packed is the only non-cubic crystal structure I’ll discuss in this article. I have a full explanation of each Bravais Lattice so you can peruse the others at your own leisure, if you are interested. Also, here you’ll find our article about HCP explained in details.
HCP is like a hexagonal prism with 3 atoms in the center. Or you can imagine it like a hexagonal plane, stacked on top of another hexagonal plane, stacked on top of a 3rd hexagonal plane which matches the first one.
HCP actually resembles FCC in many ways. In fact, they have the same APF: 74%. Both HCP and FCC are the closest-packed ways that atoms from the same element can be arranged.
The math to prove HCP’s APF is pretty complicated, but you can find in in-depth walkthrough in the same article that I’ve calculated the other crystals’ APF.
Grains in Materials
Now we can get to crystal grains. Grains are the reason why most objects don’t “look” like a crystal to you.
You can think of each grain like a crystal of its own.
Each one of those areas is a crystal with a certain orientation, joined to another crystal with a different orientation.
Imagine that you have a pool of liquid and you want to solidify it. You might imagine that several groups of atoms cluster together and form the first unit cell at different places in the liquid.
Each of these original nucleation points will eventually be the center of a grain. As other atoms join onto the existing crystal, each grain grows until it touches another grain. The end result is a material that is made of many different crystals with slightly different orientation: a polycrystal.
In many cases, a polycrystal is good because it ensures that the material has the same properties in every direction. In other cases, a single crystal is better–however, the only way to make a single crystal is if you had such control over your liquid that you could ensure that only one site nucleated. That’s not easy!
On the other hand, it’s usually easy to make grains smaller. If you introduce a lot of deformation in a metal, then heat it, the grains may fracture and reform into smaller grains. This is called recrystallization.
Smaller grains can also be achieved by quenching metal quickly.
Non-Crystalline Materials
So, we’ve talked about single crystals and polycrystals, which are the same kind of material that have different processing mechanisms. What about materials that don’t form crystals?
Actually, I don’t think there are any thermodynamically non-crystalline materials. As far as I know, every material will form a crystal if given enough time and energy for the atoms to move around. However, this time scale may be nearly infinite at room temperature.
Let’s look at glass, which is basically the definition of a non-crystalline material. Materials which are not crystalline are called amorphous solids, or glasses. Window glass is the most common amorphous solid, but obsidian, some kinds of porcelain, and bulk metallic glasses may also be considered glass because they have a random arrangement of atoms, rather than a repeating array of atoms.
And yet, window glass exists as a crystal, too. Window glass is SiO2, the same chemical that makes up quartz. The difference between quartz and glass is that quartz was given time at high temperature to crystallize. Glass was cooled quickly enough to avoid crystallization. For SiO2 to form a crystal, it actually needs to cool extremely slowly. Metals may need to be cooled in picoseconds to freeze into a glass before crystallizing.
Polymers are also usually non-crystalline. Polymers are different from other materials because they are not made of atoms, but long molecule chains. These chains can (and often do) align into an orderly pattern, but this pattern is rarely as perfect as in atomically-bonded materials like metals and ceramics. Polymers are usually considered “semicrystalline,” although they can also be completely amorphous.
Why Are Crystals So Important?
The existence of crystals carries several implications that you may never have thought of.
Why do materials have melting points? And what materials don’t have melting points? If you’ve heated up a plastic toy or seen glass melt, you’ll notice that amorphous materials like plastic and glass don’t really have a distinct melting point. They shift very gradually from solid to liquid.
Crystalline materials like metal or ice have an abrupt melting point. This is because all the atoms are at the same distance from each other–and have the same bond strength. When there is enough thermal energy, all the bonds break at once, leading to distinct melting. Amorphous solids have atoms at all different distances from each other, so some bonds break before others. Crystallinity gives a clear melting point.
How about ductility? Ignore polymers for a moment since their deformation is special. It is possible to make an amorphous metal (called bulk metallic glass, or BMG) rather than the typical polycrystalline metal. Amorphous metals can’t have atomic rows slip past each other, so they are very brittle.
However, since energy is not lost to dislocations, amorphous metals can bounce much higher than regular metals.
Even when comparing one polycrystalline material to another, the grain size, shape, and orientation can make huge differences.
For example, smaller grains make a material stronger at room temperature. You can read this article for a full explanation of this effect, called the Hall-Petch Effect.
On the other hand, at higher temperatures, smaller grains make a material more susceptible to creep because atoms can diffuse faster along grain boundaries.
Grain boundaries are also prime locations for precipitates to form.
There are hundreds or thousands of applications where grains matter, but I’ll give you one example from my own research in superalloys. Since this is copied from my article on superalloys, I’ll put this in collapsable text:
Why Grains Matter in Superalloys. Click here to find out!
Superalloys can have 3 types of grain patterns: equiaxed polycrystalline, columnar polycrystalline, and single crystal.
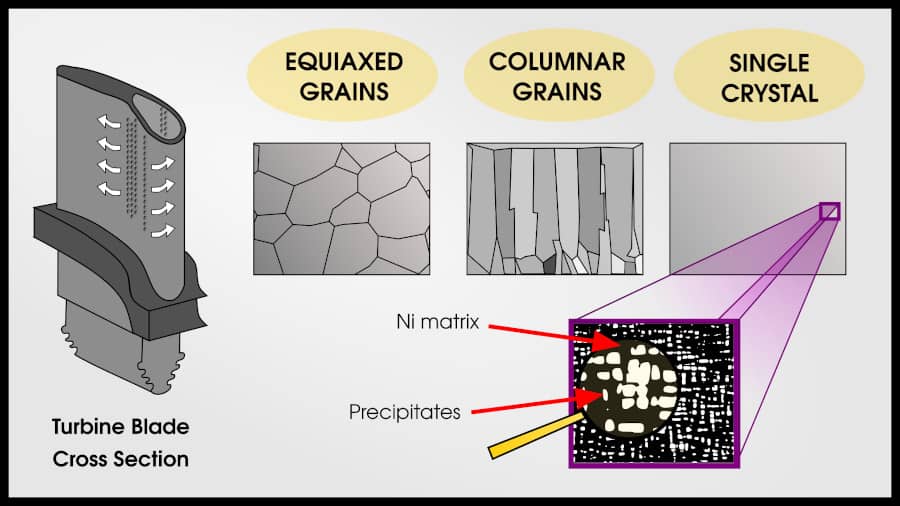
Equiaxed grains are the “default” pattern for metals. Each grain is roughly the same size and shape. Most methods of solidifying from liquid will result in an equiaxed polycrystal.
Columnar grains are more creep-resistant than equiaxed grains. In the direction of stress, there are no grain boundaries. Columnar grains are created by slowly changing the temperature gradient so that an initial set of polycrystalline grains forms, but then the liquid on top of these grains solidify in the same pattern.
The end result is that same number of grains as the initial nucleation, but each grain travels the whole length of the turbine blade.
A single crystal turbine blade has the best creep properties for three reasons:
- There are no grain boundaries at all, which is good for creep
- Sometimes “bad” phases precipitate at the grain boundaries, so removing grain boundaries avoids these phases
- The crystal can be oriented so that the maximum strength is in the direction of maximum stress
When you have a crystal, the strength of the crystal is not uniform. Force at a 90° angle will not necessarily produce the same displacement as force at a 45° angle.
However, most metals you see in real life are polycrystalline. When you average thousands or millions of grains, the end result has an average strength in all directions.
With a single crystal, there is no average. If the turbine blade will only experience force from one direction, you can orient the crystal so that the strongest crystal direction is in the same direction as the force.
Some materials, such as carbon, can have multiple crystal structures. These are called polymorphs. Carbon can exist as graphite or diamond (or other forms). SiO2 can be quartz or glass. Tin can be its regular shape or a brittle powder. Shape memory alloys work by changing crystal structure. Steel is hardened by changing crystal structure.
The most fundamental aspect of materials science, in my opinion, is structure. Structure starts with crystals.
How Are Crystals Characterized?
There are many ways to measure crystal structure, but the easiest is X-Ray Diffraction (XRD). XRD tells you the spacing between atoms.
Since once you know the spacing between atoms, you can figure out what crystal structure is present. This can be a great tool for figuring out what kind of material you have, or what phases exist.
Another method which can tell grain orientation is Electron Backscatter Diffraction (EBSD), a technique used in Scanning Electron Microscopy (SEM). EBSD can tell you each grain orientation by a similar method as XRD.
Grains can also be seen regularly in the SEM. If you put an acid on metal, the grain boundaries will have higher energy and the acid will preferentially etch these, showing grain boundaries clearly. Once the metal is etched, grains may be possible to see with the naked eye.
Here is a picture from one of our own samples, with equiaxed grains and dendrites.

Final Thoughts
Crystals are one of the most important concepts in materials science, and so few people know about them! Crystals are everywhere, from metal to ceramics. Even polymers or some organic materials like wood can be considered semi-crystalline.
A very important concept in crystals is crystal grains, which are the result of multiple polycrystals growing together.
Crystal structure and grains have a huge effect on properties, affecting everything from melting point to ductility to conductivity.
References and Further Reading
If you’re new to materials science, welcome! Crystals are a fundamental concept that you might encounter in high school or in your first day of materials science class, so I hope this article didn’t overwhelm you! If you want more information about materials science, I recommend this article which explains what materials science is, or this article which helps you decide if materials science is the right major for you.
This article which explains the materials science tetrahedron will tell you about the 4 areas of materials science: processing, structure, properties, and performance. Crystallography is essential to structure.
If you want more applications for how different crystal structures can impact properties, (and how materials science caused Napoleon to fail his invasion of Russia) you may be interested in this article about polymorphism.
In the beginning of the article, I derived atomic packing factor (APF). This is an important concept in your introductory materials science class, so if you want a full explanation of APF, check out this article.
If you’re a bit more advanced in materials science and you’re interested in crystallography, here is the full list of my crystallography articles, listed in order of increasing difficulty.
Introduction to Bravais Lattices
What is the Difference Between “Crystal Structure” and “Bravais Lattice”
Atomic Packing Factor
How to Read Miller Indices
How to Read Hexagonal Miller-Bravais Indices
Close-Packed Crystals and Stacking Order
Interstitial Sites
Primitive Cells
How to Read Crystallography Notation
What are Point Groups
List of Point Groups
Close-Packed Crystals and Stacking Order
Interstitial Sites
Primitive Cells
How to Read Crystallography Notation
What are Point Groups
List of Point Groups
What are Space Groups
List of Space Groups
The 7 Crystal Systems
If you are interested in more details about any specific crystal structure, I have written individual articles about simple crystal structures which correspond to each of the 14 Bravais lattices:
1. Simple Cubic
2. Face-Centered Cubic
2a. Diamond Cubic
3. Body-Centered Cubic
4. Simple Hexagonal
4a. Hexagonal Close-Packed
4b. Double Hexagonal Close-Packed (La-type)
5. Rhombohedral
5a. Rhombohedral Close-Packed (Sm-type)
6. Simple Tetragonal
7. Body-Centered Tetragonal
7a. Diamond Tetragonal (White Tin)
8. Simple Orthorhombic
9. Base-Centered Orthorhombic
10. Face-Centered Orthorhombic
11. Body-Centered Orthorhombic
12. Simple Monoclinic
13. Base-Centered Monoclinic
14. Triclinic