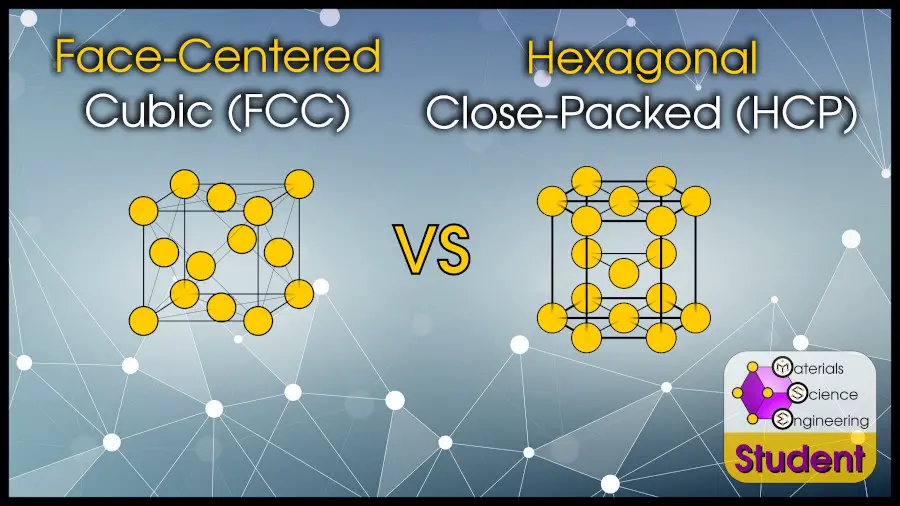
We’ve already covered the difference between the common cubic crystals (FCC and BCC), so now it’s time to discuss the difference between the common close-packed crystals (FCC and HCP).
You might think a face-centered cubic (FCC) crystal wouldn’t have much in common with a hexagonal close-packed (HCP) crystal, but by certain definitions, they are actually the same thing!
FCC and HCP are both close-packed with a 74% atomic packing factor, 12 nearest neighbors, and the same interstitial sites. However, HCP only has 3 slip systems, while FCC has 12 slip systems, which lead to very different mechanical properties.
The most direct difference between FCC and HCP crystals is in the atomic arrangements. The face-centered cubic structure is a cube with an atom at all 8 corner positions, and at the center of all 6 faces. The hexagonal close-packed structure is a hexagon with an atom at all 12 corner positions, an atom on the top and bottom face, and 3 atoms in the center.
FCC and HCP also have many different measurements within the unit cell, as shown in the table below.
| Crystal Structure | FCC | HCP |
| Unit Cell Type | Cubic | Hexagonal |
| Relationship Between Cube Edge Length a and the Atomic Radius R | a = 2R√2 | a = 2R |
| Close-Packed Structure | Yes | Yes |
| Atomic Packing Factor (APF) | 74% | 74% |
| Coordination Number | 12 | 12 |
| Number of Atoms per Unit Cell | 4 | 6 |
| Number of Octahedral Interstitial Sites | 4 | 6 |
| Number of Tetrahedral Interstitial Sites | 8 | 12 |
Outline
What is the Packing Difference and Stacking Faults Between FCC and HCP?
Both FCC and HCP are close-packed, which means they have the maximum theoretical packing density of about 74%. You can check this article for details about this calculation for atomic packing factor.
The difference between FCC and HCP lies in the close-packed stacking order.
Consider the close-packed plane, which has a hexagonal 2D arrangement. Now, if you add a layer on top of it, the atoms in this layer will have to fit between the gaps in the first layer. As you can see, there are 2 possibilities.
In total, there are 3 ways to orient each close-packed layer–we name these arrangements by the letters A, B, and C.
If you modeled atoms as simple spheres, there would only be one rule for stacking: the same letter can’t repeat. Otherwise, the order could be random, with no repeating pattern. If this were the case, then there would be no difference between FCC and HCP.
However, due to interatomic forces, the layer orders are not random, and they do repeat. If the layers repeat AB-AB-AB… then the crystal is HCP. If the layers repeat ABC-ABC-ABC…then the crystal is FCC.
Of course it’s possible for the crystal to have a defect, such as putting a C layer where there is supposed to be a B layer. This kind of defect is called a stacking fault.
If you want to read more about stacking faults and other close-packed structures (such as 9R), you may be interested in my in-depth article about close-packed crystals.
Slip Systems in FCC and HCP
FCC metals tend to be more ductile than HCP metals because of their different slip systems.
The basic requirement for ductility is to have 5 independent slip systems. (I’d recommend reading “Kelly & Knowles, Crystallography and Crystal Defects” if you want to prove this). If you don’t understand Miller Indices, this next section will be hard to follow. When reading indices for hexagonal crystals, I’ll use the Miller-Bravais system.
FCC crystals are close-packed along the planes, and the
direction within that plane. Since atoms are closely packed along these directions, these are the slip planes and slip directions. Overall, we call the slip system
. Atoms are much more likely to slip in these directions because they are closer-packed.
There are 4 different planes in the family, and 3 different directions in the
family, for a total of 12 independent slip systems. This is more than the requisite 5, so FCC crystals are ductile.
HCP crystals have only 1 close packed plane: the plane. There are 3 close packed directions in the
family. Thus, HCP structures only have 3 independent slip systems, which is less than the 5 required for ductility.
However, it is possible for HCP crystals to activate additional slip systems such as along in some metals.
| Name of a Slip System | Number of Slip Systems | Slip Plane | Slip Direction |
| Basal | 3 | ||
| Prismatic | 3 | ||
| Pyramidal | 12 |
These may be thermally activated and thus give some HCP metals a ductile-to-brittle transformation temperature (DBTT), which has been studied in Zn and Mg alloys. HCP metals usually do not display a DBTT.
One additional method which allows HCP metals to have ductility (despite having fewer than 5 slip systems) is by twinning.
Twinning is fundamentally different from slip and is more common in HCP crystals than FCC crystals. Even when twinning is possible in FCC metals, slip is usually “easier” to accommodate any deformation, so that’s the path atoms take.
In FCC metals twinning is linked to having a “low stacking fault energy (SFE).” A low SFE means that stacking faults are more common–in other words, the crystal structure is somewhere between FCC and HCP.
Interstitial Sites in FCC and HCP
Because FCC and HCP are both composed of close-packed layers, they have the same type and number of interstitial sites–the only difference is the location of these interstitial sites.
You already know that unit cells of metals are not fully packed (74% for FCC and HCP), which means they have some empty space.
Smaller atoms can fit in these spaces. Because of the different interstitial sites, different atoms can form different interstitial alloys depending on the crystal structure.
As a rule of thumb, atoms that fit in interstitial sites should be less than 15% of the size of atoms in regular sites. In fact, the exact radius ratio also determines which kind of interstitial site can be occupied.
The two main types of interstitial sites are octahedral and tetrahedral.
These sites are named because of their nearest neighbors. Octahedral sites have 6 nearest neighbors, and tetrahedral sites have 4 nearest neighbors.
You can read all about interstitial sites in this article, but here’s a summary of the interstitial sites regarding FCC and HCP crystals. If you want to prove these numbers, check out that article.
| Crystal Structure | FCC | HCP |
| Number and Size of Octahedral Voids | 4 voids, r = 0.414 R | 6 voids, r = 0. 414 R |
| Number and Size of Tetrahedral Voids | 8 voids, r = 0.225 R | 12 voids, r = 0.225 R |
Examples of FCC and HCP Elements
At room temperature, some common FCC metals are aluminum, nickel, and copper. Some common HCP metals are cobalt, magnesium, and titanium.
Here is a list of all the elements which are FCC, BCC, or HCP at room temperature.
Face-Centered Cubic (FCC) elements:
Body-Centered Cubic (BCC) elements:
Hexagonal Close-Packed (HCP) elements:
In general, alloys with these metals will have the same crystal structure as the most common element. However, there are always exceptions. (For example, cobalt and iron can both be FCC when heavily alloyed, especially with nickel).
Final Thoughts
Now you know all the differences between FCC and HCP! You also know many common materials that take each form. Now you see, even though FCC and HCP are both close-packed, the symmetry difference between them leads to different mechanical properties.
References and Further Reading
If you’re reading this article as an introductory student in materials science, welcome! I hope you can find many other useful articles on this website.
If you’re reading this article because you’re taking a class on structures, you may be interested in my other crystallography articles. Here is this list, in recommended reading order:
Introduction to Bravais Lattices
What is the Difference Between “Crystal Structure” and “Bravais Lattice”
Atomic Packing Factor
How to Read Miller Indices
How to Read Hexagonal Miller-Bravais Indices
Close-Packed Crystals and Stacking Order
Interstitial Sites
Primitive Cells
How to Read Crystallography Notation
What are Point Groups
List of Point Groups
What are Space Groups
List of Space Groups
The 7 Crystal Systems
If you are interested in more details about any specific crystal structure, I have written individual articles about simple crystal structures which correspond to each of the 14 Bravais lattices:
1. Simple Cubic
2. Face-Centered Cubic
2a. Diamond Cubic
3. Body-Centered Cubic
4. Simple Hexagonal
4a. Hexagonal Close-Packed
4b. Double Hexagonal Close-Packed (La-type)
5. Rhombohedral
5a. Rhombohedral Close-Packed (Sm-type)
6. Simple Tetragonal
7. Body-Centered Tetragonal
7a. Diamond Tetragonal (White Tin)
8. Simple Orthorhombic
9. Base-Centered Orthorhombic
10. Face-Centered Orthorhombic
11. Body-Centered Orthorhombic
12. Simple Monoclinic
13. Base-Centered Monoclinic
14. Triclinic