The Simple Hexagonal (abbreviated SH in this article) is a crystal structure which has a single-atom basis on the hexagonal Bravais lattice. There are many other crystal structures which also have a hexagonal Bravais lattice (such as the very common hexagonal close-packed), and simple hexagonal is just one of these. The simple hexagonal crystal belongs to space group #191 or P6/mmm, Strukturbericht Af, and Pearson symbol hP1. The prototype for the simple hexagonal crystal is γ-HgSn6-10.
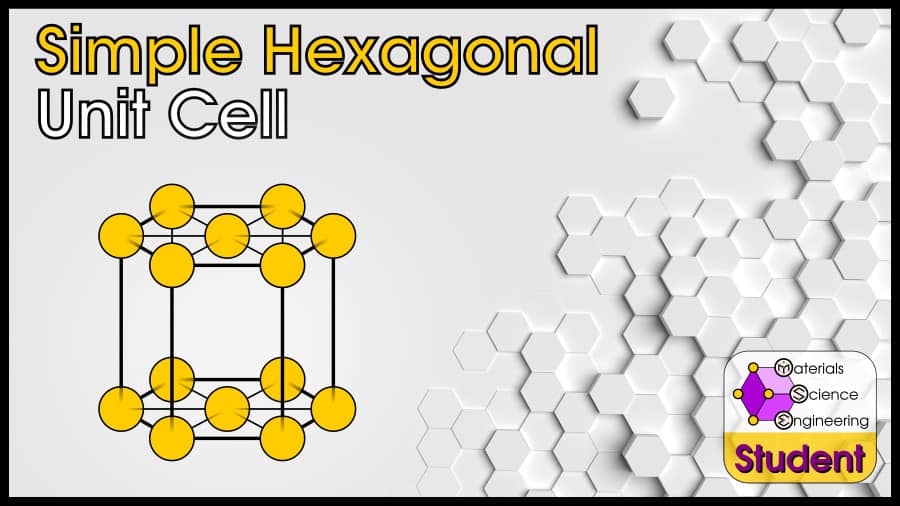
You may see the simple hexagonal unit cell drawn in the conventional way, or the primitive way.
The Simple Hexagonal (SH) unit cell can be imagined as a hexagonal prism with an atom on all 12 corners, and both faces. It is an uncommon crystal structure that doesn’t show up in any pure elements, but it does exist in some alloys. Simple hexagonal has 3 atoms per unit cell (or 1 per primitive cell), lattice constant a = 2R, Coordination Number CN = 6 (or 8), and Atomic Packing Factor APF = 61%.
Since this is an unusual crystal structure, I will assume that you are a somewhat advanced student in materials science, and are looking for quick facts. If you are new to materials science and don’t understand something in this article, I’ve made a similar article for many common crystal structures. You can reference my articles on the FCC, BCC, or HCP crystals which are aimed at beginners in materials science and explain terms like APF and CN.
Outline
Common Examples of Simple Hexagonal Materials
Simple hexagonal is a rare crystal structure which does not naturally occur in any pure elements (although it is possible to create a metastable, high pressure phase of silicon with the simple hexagonal crystal structure).
Of course, the prototype for the crystal structure is γ-HgSn6-10, which is a mercury tin alloy (substitutional solid solution) with mostly tin and about 10-17 at.% mercury.
Other alloys that can take the simple hexagonal crystal structure are BiIn, CdSn19, In7Sb3, and InSb. The phases γSn-In, γSn-Hg, βSn-Hg, and βSn-Cd can also have this crystal structure.
Remember that these are disordered structures–even though there are two elements, each element occupies a random position in the simple hexagonal crystal. If the structure were ordered so that one atom always occupied a specific positions, this would be a different crystal structure (and would be called an intermetallic compound, rather than an alloy).
Simple Hexagonal Coordination Number
The simple hexagonal unit cell is close-packed within the planes. That means there are 6 nearest neighbors (NNs) in the plane. There are also 2 atoms above and below, but if these are farther, the CN is still just 6.
This, however, assumes that the hexagonal unit cell has a longer vertical axis–in other words, lattice constants a and b are the same length (by definition, this is true), but lattice constant c is longer. We can describe this using a c/a ratio.
If the c/a ratio is 1 (so all 3 lattice parameters have the same length), the CN = 8. If the c/a ratio is smaller than 1 (c is smaller than a), the CN will only be 2.
For simple hexagonal silicon, the c/a ratio is almost one, so the CN ~ 8.
Simple Hexagonal Lattice Constants
The conventional simple hexagonal lattice is a hexagonal prism. However, we can also define a “primitive” simple hexagonal cell, which is ⅓ of the size of the regular cell. This primitive cell has 3 independent axes, so that’s how we define our lattice constants.
By definition, axes a and b are the same length (so we only talk about a) and have an angle of 120º to each other. Since we use the hard sphere model, where close-packed atoms touch, this distance is twice the atomic radius.
The c axis can be larger, smaller, or equal to the a axis–which defines the c/a ratio in hexagonal crystals. In the most common hexagonal crystal, Hexagonal Close-Packed (HCP), the c/a ratio is about 1.6.
In simple hexagonal crystals, however, there is no reason for c to be different than a and b. Indeed, in simple hexagonal silicon, the c/a ratio is ~1.
If you wanted to describe the simple hexagonal crystal with math, you would describe the cell with the primitive vectors:
Simple Hexagonal Atomic Packing Factor
If we assume that the c/a ratio = 1, then it is possible to calculate the simple hexagonal APF for an ideal simple hexagonal unit cell.
To make the calculations simpler, I will use the primitive cell. This is a parallelpiped with angles of 60º, 120º, and 90º.
The volume of the primitive cell is the area of the rhombus, times the height. The rhombus is just two equilateral triangles put together, so it has an area of . Since we assume that the height, c, is also a, its volume becomes
.
There is 1 atom split between the 8 corners. The area of a sphere is .
We know that , so we get
61% is a higher packing than simple cubic’s 52%, but it’s still lower than BCC’s 68% or the maximum close-packed 74%.
Final Thoughts
The Simple Hexagonal unit cell is a somewhat unusual way that atoms can be arranged in solids. Although there are no pure elements that exhibit this structure at room temperature and pressure, it does exist in high-pressure silicon and some alloys.
Summary table of simple hexagonal unit cell characteristics.
| Crystal Structure | Simple Hexagonal |
| Unit Cell Type | Hexagonal |
| Relationship Between Cube Edge Length a and the Atomic Radius R | a = 2R |
| Close-Packed Structure | No |
| Atomic Packing Factor (APF) | 61% |
| Coordination Number | 8 (6+2) |
| Number of Atoms per Conventional Unit Cell | 3 |
References and Further Reading
If you want to know more about the basics of crystallography, check out this article about crystals and grains.
If you weren’t sure about the difference between crystal structure and Bravais lattice, check out this article.
I also mentioned atomic packing factor (APF) earlier in this article. This is an important concept in your introductory materials science class, so if you want a full explanation of APF, check out this page.
If you’re interested in advanced crystallography or crystallography databases, you may want to check out the AFLOW crystallographic library.
For a great reference for all crystal structures, check out “The AFLOW Library of Crystallographic Prototypes.”
Single-Element Crystal Structures and the 14 Bravais Lattices
If you want to learn about specific crystal structures, here is a list of my articles about Bravais lattices and some related crystal structures for pure elements. Simple Hexagonal is one of these 14 Bravais lattices and also occurs as a crystal structure.
1. Simple Cubic
2. Face-Centered Cubic
2a. Diamond Cubic
3. Body-Centered Cubic
4. Simple Hexagonal
4a. Hexagonal Close-Packed
4b. Double Hexagonal Close-Packed (La-type)
5. Rhombohedral
5a. Rhombohedral Close-Packed (Sm-type)
6. Simple Tetragonal
7. Body-Centered Tetragonal
7a. Diamond Tetragonal (White Tin)
8. Simple Orthorhombic
9. Base-Centered Orthorhombic
10. Face-Centered Orthorhombic
11. Body-Centered Orthorhombic
12. Simple Monoclinic
13. Base-Centered Monoclinic
14. Triclinic
Other articles in my crystallography series include:
Introduction to Bravais Lattices
What is the Difference Between “Crystal Structure” and “Bravais Lattice”
Atomic Packing Factor
How to Read Miller Indices
How to Read Hexagonal Miller-Bravais Indices
Close-Packed Crystals and Stacking Order
Interstitial Sites
Primitive Cells
How to Read Crystallography Notation
What are Point Groups
List of Point Groups
What are Space Groups
List of Space Groups
The 7 Crystal Systems