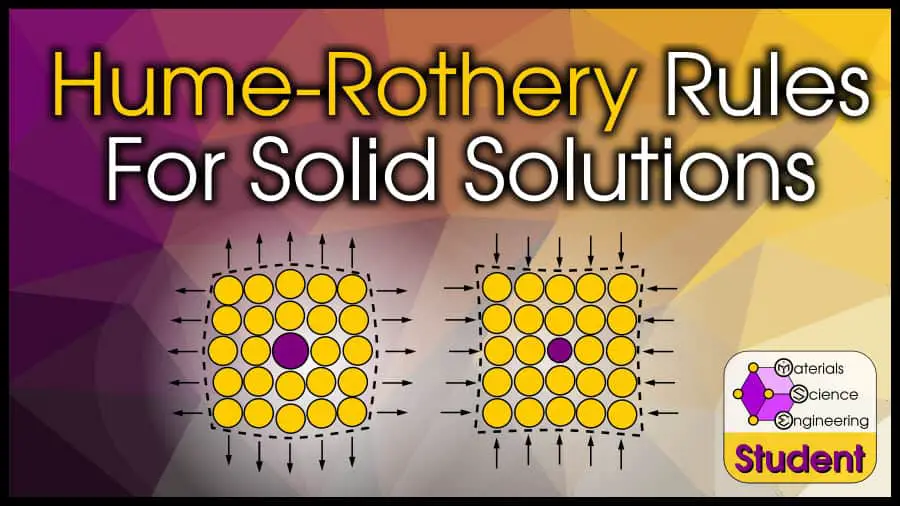
The Hume-Rothery Rules for Solid Solution – Materials Science & Engineering

The Hume-Rothery rules are a set of guidelines that can help you determine whether two elements will form a substitutional solid solution.

The Hume-Rothery rules are:

Similar atomic radii (15% difference)
Similar electronegativities
Same crystal structure
Similar valency

Of course, these are just rules of thumb. They aren’t always true, but we’ll talk about how those rules came about, and some notable exceptions. But first, let’s discuss why you might want to use them.

What Is a Substitutional Solid Solution?

A combination of metals is called an alloy. There are 3 kinds of alloys:

Substitutional solid solutions
Interstitial solid solutions
Intermetallic compounds

Substitutional alloys are the most common among engineering materials, and these are the focus of the Hume-Rothery rules.

In a solid solution, atoms from one element occupy sites in a crystal lattice (FCC, BCC, HCP, etc). This element is the solvent. Atoms from one or more elements are “dissolved” into the solvent.

In a substitutional solid solution, the solute atoms will randomly take the place of the solvent atoms. This is a 1-to-1, direct substitution.

In an interstitial solid solution, the solute atoms fit between solvent atoms. We call these “in between” positions interstitial sites. Solute atoms will typically go into interstitial sites if they are much smaller than the solvent atoms.

In an intermetallic compound, there is no solute or solvent. Instead the atoms bond stoichiometrically, just like any other compound. Because of this, most intermetallics do not behave like typical metals.

Generally, materials engineers try to avoid intermetallics.

Likewise, most metals have relatively similar ionic radii. There are only a few atoms that are small enough to occupy interstitial sites in something like iron: these small atoms are H, C, Li, Be, etc. Plain steel is an interstitial alloy of iron and carbon, but it is the only common example I can think of right now.

This leaves substitutional solid solutions as the “most important” kind of alloy. Alloys are usually improved when another element is dissolved in a substitutional site.

The Hume-Rothery rules essentially predict if a combination of metals will result in a substitutional solution instead of an interstitial solution or an intermetallic.

1. Similar Ionic Radii

Hume-Rothery’s first rule says that the ionic radii need to be within 15% of each other. That is,

$\left|\frac{r_{solvent}-r_{solute}}{r_{solvent}}\right|\le 0.15$

There are two reasons why ionic radii is important. First, if the solute atom is small enough to fit into the interstitial site of the solvent atoms, it will almost always be interstitial instead of substitutional. Simple geometry.

But even if the solute atom is bigger than the solvent atom, if the radii difference is too large, lattice strain effects will hinder solubility.

Adding a larger (or smaller) atom into an existing lattice will strain that lattice.

Each additional atom increases the strain, which limits the solubility. The lattice can only handle so much strain, until it is easier to organize the atoms into a new arrangement that minimizes the strain.

This “15%” guideline is a rule of thumb for when the lattice strains become too severe for a solid solution. For a more advanced metric, the combination of radii and electronegativity can create a Darken-Gurry map.

Chart of Ionic Radii

For your convenience, I have included a chart of atomic radii.

These are atomic radii, not ionic radii. Both metallic and ionic bonds hold materials together because of electrostatic interaction. For example, table salt is NaCl, which is Na⁺ ions bonded to Cl^– ions.

The Cl atom steals an electron from Na, so Na becomes positive and Cl becomes negative. These non-neutral atoms are called “ions.” Since Cl^– has an extra electron compared to Cl, it is larger than Cl. Likewise, Na⁺ is smaller than Na.

In metals, the atomic radii is somewhere between the radius of a lone atom, and an ionic radius. Metallic bonding is sometimes considered to be a group of positive ions glued together by a sea of free electrons.

2. Same Crystal Structures

For two elements to have appreciable solubility, they need to have the same crystal structure. You can see how it might induce strain if a substitutional atom wants to pack differently than the surrounding atoms.

The “natural” crystal structure of each element is due to quantum mechanics.

And of course, there are exceptions to this rule. For example, stainless steel is mostly iron, with about 20% chromium (substituting for iron) and less than 1% carbon (interstitial sites). Iron and chromium are typically BCC, so these stainless steels are also BCC.

However, if you add enough nickel, suddenly FCC is the more thermodynamically favorable crystal structure. Perhaps most surprisingly, nickel and chromium happily sit in random substitutional sites within the now-FCC iron lattice.

If this sounds complicated–don’t worry, it is. Many early metallurgical/materials science experiments involved complicated experiments to test and see which phases developed when you mixed metals together. Tons of research is dedicated to developing computational tools to calculate the quantum mechanics and predict the result.

Still, real-life experiments are the best way to collect this data. My own research mostly involves adding new elements to superalloys and seeing whether I get a substitutional solution or a nasty intermetallic.

However, I am not just blindly guessing elements–I use Hume-Rothery’s rules and more advanced computational tools to make educated predictions about which elements will be the most beneficial!

Periodic Table with Room Temperature Crystal Structures

For your convenience, I have included a chart of crystal structures for each element. If you would like to see all my references for this information, you can check out this article.

This chart lists the crystal structure for each element and has an asterisk (*) if that crystal structure is predicted (not experimentally verified). For Hume-Rothery rules, BCC, FCC, and HCP are the most important structures. For more complex crystal structures, I’ve written “complex” and the Bravais lattice; for example, Iodine resembles base-centered orthorhombic, but there are I₂ molecules at each lattice point. If you want to learn more about Bravais lattices and crystal structures, check out this article.

3. Similar Electronegativity

The next-most important similarity for solubility is electronegativity.

Electronegativity is a property that says how badly an element wants to steal an electron. Atoms with high electronegativities will take electrons from nearby atoms with lower electronegativities.

If two elements have a large electronegativity difference, they will be attracted to each other because one atom will pull on another’s electron. This causes the now-more negatively charged atom to be attracted to the now-more positively charged atom. If this happens, the material is chemically bonded (ionic or covalent), instead of metallically bonded.

That isn’t a solution, that’s a compound! The atoms will be arranged in an ordered intermetallic.

So how much electronegativity difference is okay? Any electronegativity difference will cause atoms to be attracted to each other and form an ordered compound. However, entropy wants the atoms to be mixed randomly, rather than in a particular order.

As long as the electronegativity difference is small enough that entropy “wins,” the atoms will form a solution instead of a compound. It turns out that this difference is about 0.3 on the Pauling scale (entropy is powerful!)

In an equation, this means

$\left|\frac{\chi _{solvent}-\chi _{solute}}{\chi _{solvent}}\right|\le 0.3$

Chart of electronegativity

If the atoms have a not-small electronegativity difference, they will be more likely to form intermetallic compounds instead of solid solution. An electronegativity difference generally means the atoms will be attracted to each other. If the potential energy decrease from organizing the atoms is stronger than the entropy decrease from mixing the atoms, the alloy will become an intermetallic.

Click here for a chemistry refresher on solutions and mixtures!

In chemistry, you probably learned about chemical bonds, solutions, and mixtures.

A chemical bond occurs when two elements come together and their electrons interact. This interaction can dramatically change the properties of the two atoms. Since it makes more sense to consider the new material as one “thing,” we call it a compound. Compounds are made of more than 1 element, chemically bonded into a single phase.

For more on physical vs chemical bonds, the preview for this paper has a nice table.

I now want to introduce the idea of phases. The idea that a material is all “one thing” is the same as saying it is “one phase.” A phase is any portion of matter that shares all of the same properties. For example, if you selected some atoms of water, you would not be able to tell the difference between water somewhere else.

If you added salt, the salt atoms would spread out evenly through the water. Before the salt is added to water, it is clearly a different phase. Table salt is a solid, crystalline arrangement of sodium and chlorine atoms. But once you add salt and mix the water, the sodium and chlorine atoms split apart (we call these “ions”) and “become one” with the water.

Again, everything is one phase because any region of the salt water has the same properties as any other region. We call this a solution.

A solution occurs when one substance dissolves another substance, the way water dissolves salt. In a solution, one phase absorbs another. You have one of the same phases which is now chemically different, but physically almost the same.

Water and salt yields salt water. Salt water and more water yields less-salty water. The dissolved salt would spread throughout all of the water, so as long as some atoms of water touch other atoms of water, the result is still a single phase.

But if you add oil to water, it is easy to distinguish from water. Thus, water is one phase and oil is another phase.

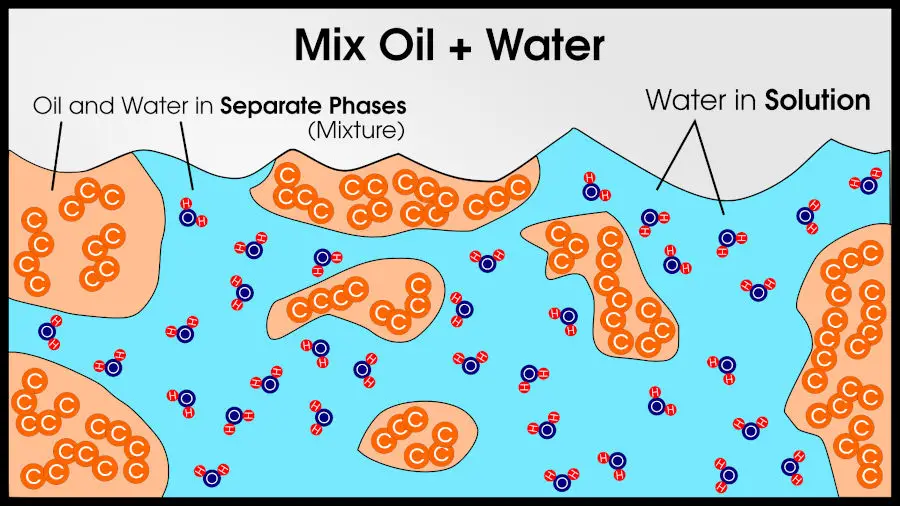
Different phases can also be chemically identical. Water and ice are chemically identical (they are made of the same atoms, 2 hydrogen per 1 oxygen), but since it’s still easy to tell the difference between water and ice, they are different phases.

Compounds and solutions (and elements) are made of only a single phase. Mixtures have multiple phases.

For example, you could make a mixture of 3 compounds: salt, water, and oil. You will end up with two phases: pure oil and a solution of salt water. Since there are two phases, the final result is a mixture, according to basic chemistry definitions.

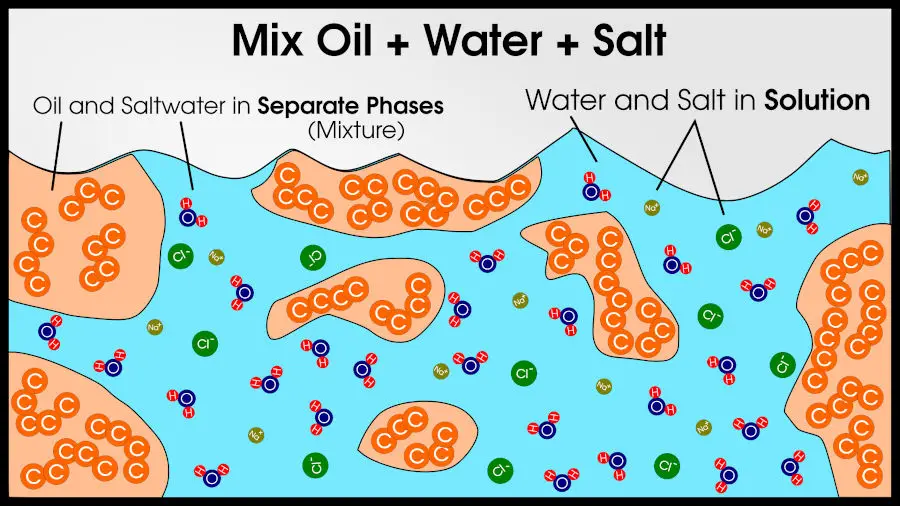
In a compound, combining 2 or more phases yields a completely different phase.

In a solution, combining 2 or more phases yields one of the original phases.

In a mixture, combining 2 or more phases does nothing. Each phase stays distinct.

If you mix sand and water, it is easy to distinguish which part is sand and which part is water. There is no “sandy water,” just a mixture of sand and water.

For your convenience, I have included a chart of electronegativity, reproduced from this website.

Combining Radii and Electronegativity: Darken-Gurry Maps

If you want to see the relationship between ionic radii and electronegativity, click below to expand the explanation of Darken-Gurry Maps. For my more casual readers, move along!

Click here to learn about Darken-Gurry maps!

The basic idea of Darken-Gurry maps is to combine the effects of electronegativity ( $\chi$ ) and radius ( $r$ ). If you plot these on a chart, atoms that are closer together should be more likely to be soluble.

Here is a Darken-Gurry map from the Encyclopedia of Materials.

Now, you could draw circles. For example, suppose I wanted to know which elements were within 7.5% radius and 0.2 electronegativity. I could choose the radius and electronegativity for my chosen solvent atom, and graph

$\left|\frac{\chi _{solvent}-\chi _{solute}}{0.2}\right|^2+\left|\frac{r_{solvent}-r_{solute}}{0.075\cdot \:r_{solvent}}\right|^2=1$

The chosen solute element will be at the center of the circle, and any other elements within the circle should be highly soluble.

According to this presentation provided by Shenyang National Laboratory for Materials Science, elements within 15% radius and 0.4 electronegativity should be at least 5% soluble. So if you drew the circle

$\left|\frac{\chi _{solvent}-\chi _{solute}}{0.4}\right|^2+\left|\frac{r_{solvent}-r_{solute}}{0.15\cdot \:r_{solvent}}\right|^2=1$

Anything that fell inside this circle would be at least 5% soluble.

The Darken-Gurry map is pretty good, but there are still exceptions to the rule. One notable exception is aluminum, which tends to be more soluble than the map would predict.

4. Similar Valency

The final Hume-Rothery rule–with the most exceptions–is that the atoms should have a similar valency. Valency is the number of electrons in the atom’s outer shell.

In other words, mutually soluble elements will typically be in the same column of the periodic table. They could also be one or two columns off, but maximum solubility will happen if they have the same valency.

Personally, I think the valency rule is not as important as the other Hume-Rothery rules, because

It has the most exceptions.
Atoms with the same valencies tend to be very similar in other areas. The number of outer-shell electrons influences crystal structure, ionic radii, and electronegativity.

There is one interesting point that Hume-Rothery made about valency, which is often overlooked. He suggests that elements are not equally likely to dissolve each other. The lower-valence elements (left side of the periodic table) are more likely to dissolve higher valence elements (right side) than vice versa.

A “chart of valency” is literally just the periodic table.

Are Hume-Rothery Rules Still Important?

As a student who may need to intuitively guess how materials will behave on a test, Hume-Rothery rules are very useful.

In modern research however, we have more advanced tools. I already showed a glimpse of Darken-Gurry maps, which is one improvement. We also have computational tools such as CALPHAD which can predict much more complex phases. Hume-Rothery rules only apply in simple cases, and phase diagrams have already been experimentally created for all the simple cases. For situations in which Hume-Rothery rules would apply, you can just look up the answer in a database.

Nonetheless, I think Hume-Rothery rules are an important first step in alloy design. Before you scour the library looking for a particular phase diagram, or boot up CALPHAD for the computer to make a guess, a materials scientist can use these rules to eliminate alloys that “obviously” won’t work.

References and Further Reading

Click here to read Hume-Rothery’s original paper. You can also check out Hume-Rothery’s follow-up paper.

A quick run through of real-life applications of Hume-Rothery rules is presented by Dr. Bhadeshia at Cambridge.

Shenyang National Laboratory for Materials Science hosts an advanced presentation on Hume-Rothery rules and metals.

Here you’ll find a research paper combining Hume-Rothery rules with neural networks.

There’s even a textbook (I can’t vouch for it because I haven’t read it, so that’s not an affiliate link).