
I feel like every time I learn something about magnetism, I realize that my previous understanding was somehow incorrect or oversimplified. As I’m writing this, I have finished my PhD classes, so hopefully I’m done re-learning magnetic properties.
All materials have some form of magnetism. Elements can be diamagnetic, paramagnetic, or ferromagnetic. Compounds made of multiple elements can also be ferrimagnetic or antiferromagnetic.
In this article, I want to tell you everything I wish I had learned about magnetic materials, the first time. I’m going to make things as simple as possible without oversimplifying in such a way that you will have to unlearn something. If you pursue a PhD and one day your knowledge of magnetism exceeds mine, I hope that you will not need to unlearn anything that you’ve read here.
That said, I am a materials scientist who specializes in mechanical properties, not magnetic properties. I’ll provide a short background on magnetic fields and the quantum mechanical basis for magnetism, but if you really want those details you’re better off asking a physicist.
Outline
What is Magnetism?
“Magnetism” is a broad term that relates to half of the electromagnetic force. You intuitively know what a magnet is, so you have some idea of forces of attraction and repulsion. The best way to describe magnetism is by using “magnetic fields.”
Magnetic fields are a topic that you may have learned in high school but possibly forgot about, so here’s a quick refresher.
Click here to learn about magnetic fields.
Magnetic fields work just like electric fields. There is a magnetic source and sink–we call these the “north pole” and “south pole” of a magnet.
Magnetic field lines travel from the north pole to the south pole (or from the south pole to the north pole, you do you).
Every north and south pole of a magnet needs to also have its opposite side, but field lines can even travel from one magnet to a different one.
Magnetic field lines don’t “really” exist. They are a conceptual tool to help us understand magnetic behavior. The field lines track potential energy.
Basically, the north magnetic pole would reduce its potential energy by moving closer to the south pole, if it moved in the direction indicated by the field lines. A bar magnet can’t bring its north and south poles closer together, but it can align its north or south poles to a different magnet’s south or north poles.
I’m sure you knew that, but when you have multiple magnets and complex arrangements of north and south poles, it’s easier to just consider how magnetic fields interact. This is especially useful when dealing with the full electromagnetism, because electricity can also generate magnetic fields.
Not only do magnetic field lines indicate the polarity (north vs south) of a magnet, they also indicate the strength, or flux, of a magnetic field. The closer together lines are drawn, the stronger the magnetic field.
For example, in the space between these atoms, the field lines are roughly equally spaced, so the magnetic flux is roughly constant. Close to any individual pole, however, you will see that the field lines come very close together. This indicates that the poles have the strongest magnetic force.
In other words, an object that would be attracted to a south pole, when placed anywhere, would follow the field lines until it reached its minimum potential energy at one of the south poles of the magnet.
Sorry if that wasn’t the best explanation, there are whole university classes that discuss electrical and magnetic fields.
So if you understand what a magnetic field is, then a “magnetic material” would be a material that reduces its potential energy by following the field lines. In other words, it would be attracted to a north or south pole.
At least, that’s how most people use the word “magnetic.” In reality, every atom is magnetic. However, there are different types of atomic magnetism–and these magnetic effects get even more complicated when atoms are arranged in crystal structures.
If you’re advanced in your studies, you may know that the type of magnetism that sticks to magnets is called ferromagnetism.
If you’re really advanced, you might know that ferromagnetism is not the only kind of magnetic material. In fact, most refrigerator magnets are actually ferrimagnets.
Whatever your current understanding of magnetic properties, this post is going to start at the basics and cover it all!
The Origin of Magnetism
Before we dive into types of magnetism, I need to address the fundamental origin of magnetism.
Magnetism is a quantum-mechanical effect that is related to electron spin. Quantum mechanics is notoriously difficult to explain in an intuitive way, but I’ll do my best to simplify things without presenting falsehoods.
Click here for an explanation of Quantum Numbers.
Every electron in an atom has a specific set of quantum numbers. You might have learned this in high school chemistry.
The principle quantum number, , describes the electron shell.
is the closest shell to the atom. Among currently discovered elements 7 is the maximum value for
. You can see the maximum value for n for any element by seeing which row the atom is on the periodic table. For example, iron is in row 4, so
can be 1, 2, 3, or 4.
The angular (or azimuthal) quantum number, , describes the electron orbital.
can be between 0 and
.
is an s orbital,
is a p orbital,
is a d orbital,
is an f orbital,
is a g orbital, etc. For example, an electron in the 4th shell
could have 3 orbitals:
and
.
The magnetic quantum number, , ranges from
to
. For example, an electron in the d orbital
could have five values of
and
.
The spin quantum number, , can only have two values: up or down.
Perhaps misleadingly, the spin quantum number is what gives rise to magnetism. According to Hund’s rule, the electrons fill the entire orbital with the same spin, and then fill the orbital with the opposite spin. For example, iron has 6 (out of 10) electrons in its outer d suborbital. The first 5 electrons will be spin up, and the 6th will be spin down.
You can use the electron configuration to tell which electrons are in the outer shell.
You can search about electron configurations if you have forgotten, but as a quick refresher, electron configurations are written by labeling the quantum numbers, going in line of the periodic table.
The electron configuration for iron is 1s22s22p63s23p64s23d6. So you can see that iron has 6 electrons in the unfilled d orbital. In shorthand, you could back up to the nearest noble gas and write it as [Ar] 4s23d6. Co would be [Ar] s23d7, and Ga would be [Ar] 4s23d104p1.
These unpaired electrons in each atom of iron have a net spin. This is called the Bohr magneton. As you can see from this calculation for iron, iron has a theoretical bohr magneton of 4. Elements with full or empty orbitals have no net spin because every “up spin” electron is paired with a “down spin” electron, and thus the atom has a Bohr magneton of zero.
This was a very hand-wavy argument; if you want a more rigorous mathematical approach you can check out this excellent chapter on the origin of magnetic dipoles.
As you’ll see in the next section, there is a concept called “exchange interaction” which relates the Bohr magneton to the material’s magnetic properties. (Spoiler: bonding and electron sharing changes things a lot).
What Property does Magnetism Measure?
When you talk about the magnetic properties of a material, you are talking about how the material responds to an external magnetic field. We call this external magnetic field H.
The addition of all the magnetic moments in a material is called M. We can also use B, which is similar and more common, but less intuitive (I’ve explained the difference between B and M in this article).
So basically, what makes something magnetic is the fact that B changes when H changes.
Since B is a function of H, there is a slope between the two. That slope is called magnetic permeability, is the permeability of free space. That means that if you created a magnetic field
in a vacuum,
of the vacuum would be
.
A very similar measurement to permeability is susceptibility, represented by .
is the slope on the M-H curve, the same way μ is the slope on the B-H curve. (Again, you can read more about these differences in this article). The susceptibility of a vacuum is 0.
We can also define relative permeability, which is just the ratio of the material’s permeability to the permeability of free space.
Types of Magnetic Materials
Magnetic materials are defined by their response to an external field (in other words, their permeability).
There are 3 main types of magnetic materials: ferromagnetic, paramagnetic, and diamagnetic. I will also cover the other two types: ferrimagnetic and antiferromagnetic.
Diamagnets have a relative permeability slightly less than one. Paramagnets have a relative permeability slightly greater than 1. Antiferromagnets have a relative permeability almost exactly equal to 1. Ferromagnets and ferrimagnets have a very large, non-linear relative permeability.
Diamagnetism
All materials have diamagnetism. Diamagnetism is a repulsive property that arises from Lenz’s law.
Lenz’s law says that creating a magnetic field will move electrons. Moving electrons also creates a magnetic field, and the newly created magnetic field will oppose the original one.
This holds true even for electrons on an atom. For any material, exposing the material to a magnetic field will cause the electrons in the atom to move in a way that creates a tiny magnetic field in the opposite direction.
By this logic, all materials should be repelled by a magnetic field, regardless of the direction of the magnetic field. However, this repulsion is so tiny that it requires very specialized equipment to measure.
Diamagnetic materials have a Bohr magneton of zero, so diamagnetism is the only magnetic effect they experience. All materials have diamagnetism, but other forms of magnetism are stronger, so materials that also have another kind of magnetism are categorized by their strongest type.
Examples of Diamagnetic Metals with (Relative) Magnetic Permeability Values:
- Copper (Cu): μr = 0.99999
- Mercury (Hg): μr = 0.99997
- Bismuth (Bi): μr = 0.99984 – strongest diamagnetic properties
Other Diamagnetic Metals:
- Zinc (Zn)
- Magnesium (Mg)
- Gold (Au)
Examples of Diamagnetic Materials That Are Not Metals:
- Silicon (Si)
- Phosphorus (P)
- Water
- Graphite
- DNA and other proteins
Relationship between B (magnetic density flux) and H (magnetic field strength):
Paramagnetism
Diamagnetism is a weak alignment against an applied magnetic field, so paramagnetism is a weak alignment with an applied magnetic field. There are a few types of paramagnetism (see this article for more), but the net effect is the same: the electrons create a magnetic field that aligns with the external field.
In some metals, depending on quantum mechanical effects, these electrons may actually experience a stronger diamagnetic effect in addition to the paramagnetic effect. Atoms like Cu or Ag essentially experience 2 kinds of diamagnetism and 1 kind of paramagnetism, so the elements are overall diamagnetic.
In high school you may have been taught to simply calculate the Bohr magneton and declare that elements with were diamagnetic and all others were paramagnetic; unfortunately real-life quantum mechanics are not that simple and you’re better off looking up which kind of magnetism a material has (don’t worry, I have a chart later in the article).
Examples of Paramagnetics with (Relative) Magnetic Permeability Values:
- Platinium (Pt): μr = 1.00027
- Aluminum (Al): μr = 1.0000196
- Air μr = 1.00000037
Other Examples of Paramagnetic Materials:
- Sodium (Na)
- Tin (Sn)
- Oxygen (O2)
- Hydrogen (H2)
Relationship between B (magnetic density flux) and H (magnetic field strength):
Ferromagnetism
Ferromagnetic materials will also experience paramagnetic and diamagnetic effects, but the ferromagnetic effect is much greater than these effects.
Ferromagnetism arises from exchange coupling which causes the formation of magnetic domains.
Domains are regions where all of the atoms contribute their magnetic moment in the same direction.
As with several of my explanations, unfortunately I can’t provide a more intuitive answer than
There is something called the Beth-Slater model which predicts ferromagnetism based on atomic spacing and electrons in the d-orbital.
According to this model, Cobalt is actually the most ferromagnetic metal.
Quantum mechanics aside, the idea of domains is actually not too difficult to understand, if you are willing to accept their existence on faith. Domains are regions of the material where all the atoms’ moments align in the same direction.
Different domains, however, are randomly oriented at first. But when you introduce an external magnetic field, each domain aligns with that field and produces their own magnetic field. Even after you remove the external field, all of the domains reinforce each other and the material maintains its magnetic field.
This creates a property called magnetic hysteresis, which you can read all about here.
It is possible to remove the internally created magnetic field by raising the temperature of the ferromagnet. As temperature increases, the atoms (and domains) vibrate more until exchange coupling ceases and the domains can no longer maintain their non-random alignment.
This temperature is called the Cure temperature. Above the Curie temperature, ferromagnetic materials become paramagnetic.
Antiferromagnetic Materials
Antiferromagnetic materials have spin alignment like ferromagnetic materials; however, while ferromagnets align atomic magnetic moments in the same direction, antiferromagnets align the magnetic moments in opposite directions.
In other words, antiferromagnets moments perfectly pair up against each other, leading to 0 total magnetism (in theory, but in practice there are crystal defects so the moments are not perfectly opposing each other, so the total magnetic moment is greater than 0).
This phenomenon is called “spin energy superexchange.” (Superexchange is also used to describe how ferromagnetic domains align). This is a bit complicated and relies on knowledge of a few basics of quantum chemistry, so let me explain in collapsable text.
Click here to learn about superexchange in antiferromagnets.
MnO is the classic example of an antiferromagnet. The ionic ceramic has Mn2+ ions which would like to steal 2 electrons, and O2- would like to donate 2 electrons. Due to the Pauli exclusion principle, O2- must have 1 electron with spin up and one electron with spin down.
Hund’s rule states that the electrons will fill the d orbital with spins in the same direction first. Since Mn2+ has 5 unpaired electrons in the d orbital, all 5 electrons must be the same–let’s imagine they are spin up. That means that the 6th and 7th electrons must be spin down.
So, the O2- must donate its spin down electron to the Mn2+ on the left. O2- has one spin up electron remaining, which gets donated to the Mn2+ on the right. But the same reasoning I just used, if the spin up goes to the right, the other 5 electrons must be spin down.
MnO has a rock salt crystal structure. If you look at the simple cubic lattice, each Mn atom has a magnetic moment of 3, but pointing in the opposite direction as the magnetic moment of the next nearest Mn atom. Thus, all the moments cancel each other.
Just like ferromagnets become paramagnets above the Curie temperature, antiferromagnets become paramagnets above the Néel temperature. In both cases, the thermal energy causes fluctuations and randomness that can overcome the superexchange.
If you want to read a more accurate but very mathematical description of superexchange, you can check out this paper by Anderson.
There are not many practical magnetic applications for antiferromagnets (since they are essentially nonmagnetic), but they can be used as a reference point in magnetic experiments. They also have great theoretical value and may help scientists understand superconductors better.
Ferrimagnetic Materials
If you’ve ever seen a ceramic refrigerator magnet, that was probably a ferrimagnet. Ferrimagnetic materials behave very similarly to ferromagnetic materials. However, ferrimagnets work by the same indirect superexchange as antiferromagnetts.
While antferromagnets completely cancel each other out because each pair of magnetic moments are equal, ferrimagnets only have partial cancellation. Which means they really have partial magnetization.
Each magnetic moment is paired with a weaker magnetic moment in the opposite direction. Since all the strong moments line up in the same direction and the weak moments line up in the opposite direction, the strong moments win and the material has an overall magnetic moment.
Fe3O4, the oldest known magnetic material, is a ferrimagnet. This material has an inverse spinel structure with Fe3+ on tetrahedral sites, and Fe2+ and Fe3+ both occupying octahedral interstitial sites. The Fe3+ in the octrahedral and tetrahedral sites cancel each other out, but the remaining Fe2+ don’t cancel, leading to a net magnetic moment.
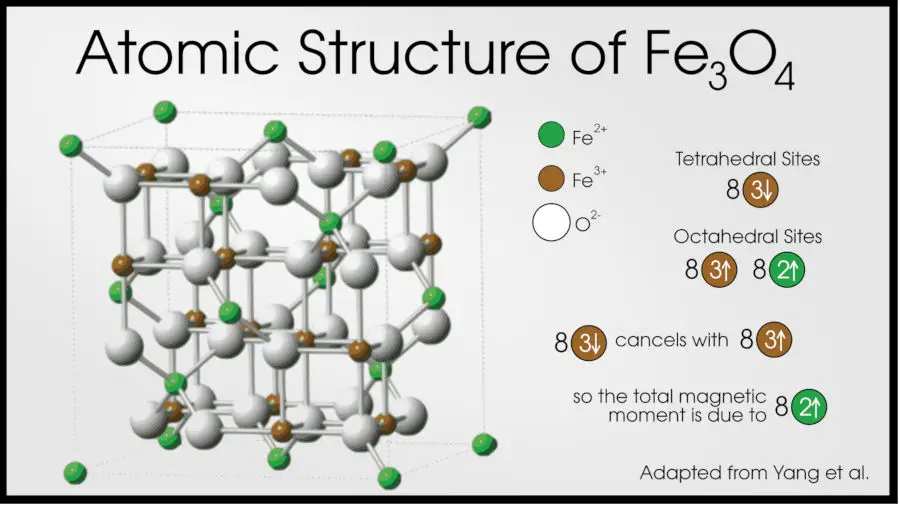
Ferrimagnets behave pretty much identically to ferromagnets, including having a Curie temperature.
If you want to read a paper by Néel himself, you can check out this one.
Final Thoughts
Now you know about all 5 types of magnetism, why magnetism exists, and examples of each kind of magnetic material.
Before you go, take a look at this handy chart which will help you remember how the magnetic moments behave in each kind of material.
References and Further Reading
Click here to learn more about magnetic hysteresis. If you want to know the difference between magnetic induction B and magnetization M, read this article.
For more math behind the origin of magnetic dipoles, I recommend this article by Professor Föll.
For more about magnetic susceptibility, you can read this article by Alan Elster or this article by Richard Fitzpatrick.
For more about the spinell structure, I recommend this article by Aditya vardhan.
If you want to read a more accurate but very mathematical description of superexchange, you can check out this paper by Anderson.
Yang et al.’s paper, which draws the structure of Fe3O4, can be found here.
Here is one of Néel’s papers about ferromagnetism and antiferromagnetism.
If you want to learn more about antiferromagnetism, Katherine Wellmon wrote this helpful article.
This page by Bruce Moscowitz has an excellent breakdown of types of magnets. He put special emphasis on temperature dependence, which I didn’t really cover in this article.
If you want to learn more about specific materials used for magnets, the University of Birmingham hosts two excellent articles on hard magnets and soft magnets.