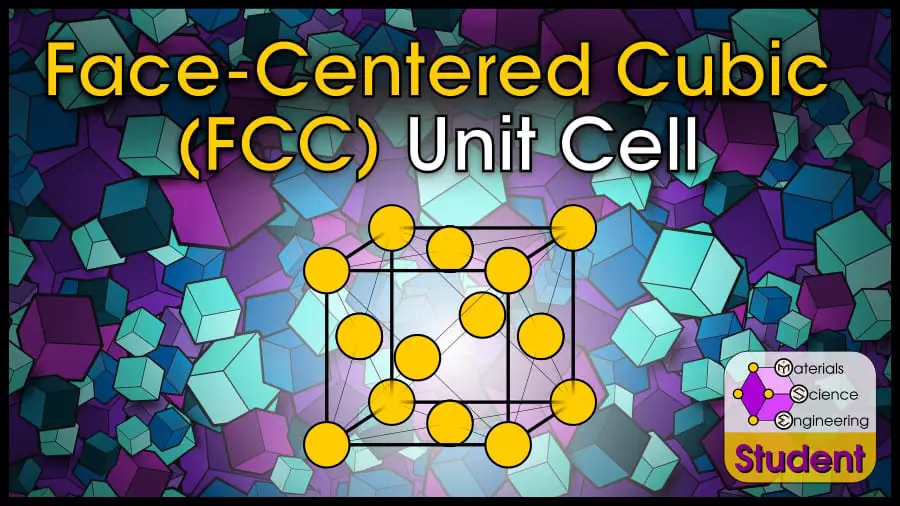
Face-Centered Cubic (FCC) Unit Cell – Materials Science & Engineering

Perhaps the most common crystal structure is Face-Centered Cubic (FCC). The crystal structure is based on the Bravais lattice of the same name, with a single atom at each lattice point on the cube’s corners and faces. FCC is one of the most stable crystal structures and has the highest packing density. In some textbooks, FCC may also be abbreviated as CCP, which stands for Cubic Close-Packed. The face-centered cubic cell belongs to space group #225 or $Fm\bar{3}m$ , Strukturbericht A₁, and Pearson symbol cF4 . Cu is the prototype for FCC.

The Face-Centered Cubic (FCC) unit cell can be imagined as a cube with an atom on each corner, and an atom on each face. It is one of the most common structures for metals. FCC has 4 atoms per unit cell, lattice constant a = 2R√2, Coordination Number CN = 12, and Atomic Packing Factor APF = 74%. FCC is a close-packed structure with ABC-ABC stacking.

Don’t worry, I’ll explain what those numbers mean and why they’re important later in the article. For now, let’s talk about which materials actually exist as face-centered cubic.

Outline

Common Examples of Face-Centered Cubic Materials
Face-Centered Cubic Coordination Number
Face-Centered Cubic Lattice Constants
Face-Centered Cubic Atomic Packing Factor
Primitive Face-Centered Cubic Unit Cell
Interstitial Sites in Face-Centered Cubic
Slip Systems in Face-Centered Cubic
Final Thoughts
References and Further Reading

Common Examples of Face-Centered Cubic Materials

Since FCC is one of the most common crystal structures, there are many materials to choose from!

Aluminum, calcium, nickel, copper, strontium, rhodium, palladium, silver, ytterbium, iridium, platinum, gold, lead, actinium, and thorium all have an FCC structure. This list is not comprehensive; FCC can also be found in high pressure/temperature phases (like lanthanum), solidified gases (like xenon), or in alloys like steel or cobalt-based superalloys.

FCC metals are usually very ductile and have no ductile-to-brittle phase transformation. If you are interested in the differences between FCC and BCC (another common structure), you may be interested in this article.

One reason that FCC has its properties is because of its high coordination number.

Face-Centered Cubic Coordination Number

Coordination Number (CN) is the number of nearest neighbors that each atom has.

In a face-centered cubic crystal, each atom has 12 nearest neighbors (NN). That’s the theoretical maximum number of NNs possible–each of those NNs contributes a bond, giving the crystal structure very high stability.

FCC has 6 next-nearest neighbors, and 24 next-next nearest neighbors.

Face-Centered Cubic Lattice Constants

The face-centered cubic lattice is a cube with an atom on each corner and each face. Using the hard sphere model, which imagines each atom as a discrete sphere, the FCC crystal has each atom touch along the face diagonal of the cube.

That means that the face diagonal has a length of $4r$ , so with a bit of geometry we find that the lattice parameter $a$ , or side length of the cube, has a length of $2\sqrt{2}r$ .

If you wanted to describe the face-centered cubic crystal with math, you would describe the cell with the vectors

$a_{1}=\frac{a}{2}\hat{y}+\frac{a}{2}\hat{z}$
$a_{2}=\frac{a}{2}\hat{x}+\frac{a}{2}\hat{z}$
$a_{3}=\frac{a}{2}\hat{x}+\frac{a}{2}\hat{x}$

These are actually primitive vectors, which you can read about in the section below.

Face-Centered Cubic Atomic Packing Factor

The Atomic Packing Factor (APF) is essentially the density of the unit cell. Since we use the hard sphere model, each point inside the cell is either part of an atom, or part of the void.

APF is basically the fraction of atoms to void. For a full article explaining APF, check out this link.

APF is the

$APF=\frac{volume\:taken\:by\:atoms}{total\:volume}$

The total volume of the unit cell is just the volume of a cube. The cube side length is a, so the volume is $a^3$ .

Now we need to count how many atoms are in each unit cell. It may look like there are 14 atoms because there are 8 corners and 6 faces, but actually the cell only intersects portions of those atoms.

If you count the portion of the atoms in the cell, 1/8th of each atom would count, and there are 8 corner atoms. $8\cdot \frac{1}{8}=1$ , so there is one full corner atom. ½ of each face atom is inside the cell, and there are 6 face atoms, so $6\cdot \frac{1}{2}=3$ .

Thus, there are 4 atoms per unit cell.

The volume of a sphere is $\frac{4}{3}\pi r^3$ . We previously established that the volume of the whole cube is $a^3$ , and since $a=2\sqrt{2}r$ , the volume of the cube is $(2\sqrt{2}r)^3$ .

Now that we’ve written everything in terms of the radius of an atom, you can see that every face-centered cubic crystal will have the same packing factor regardless of the actual element.

$APF_{FCC}=\frac{\left(\frac{8}{8}+\frac{6}{2}\right)\frac{4}{3}\pi r^3}{\left(2\sqrt{2}r\right)^3}=\frac{\pi }{3\sqrt{2}}\approx 74\%$

As you can see, face-centered cubic crystals have 74% packing. This is the highest possible packing for spheres of the same size, although it’s possible to have higher packing if you used multiple kinds of atoms of different sizes.

Since FCC has the maximum type of packing, it is a close-packed structure. The other common close-packed structure is hexagonal close-packed (HCP), although there are also lesser-known types like the close-packed rhombohedral structure found in Samarium.

Primitive Face-Centered Cubic Unit Cell

Advanced topic, click to expand!

The FCC cell that I have shown you is a conventional unit cell, not a primitive unit cell. This conventional cell has advantages because it is highly symmetric and easy for humans to understand.

However, when dealing with mathematical descriptions of crystals, it may be easier to describe the unit cell in the smallest form possible. The smallest possible unit cell is called the primitive cell. If you are interested in primitive cells, you can read all about them in this article.

The FCC primitive cell looks like this:

Here are the primitive vectors for the FCC unit cell.

$a_{1}=\frac{a}{2}\hat{y}+\frac{a}{2}\hat{z}$
$a_{2}=\frac{a}{2}\hat{x}+\frac{a}{2}\hat{z}$
$a_{3}=\frac{a}{2}\hat{x}+\frac{a}{2}\hat{y}$

Interstitial Sites in Face-Centered Cubic

Interstitial sites are the spaces inside a crystal where another kind of atom could fit. You can read all about interstitial sites in this article, but FCC has two types of interstitial sites: octahedral and tetrahedral. (Technically trigonal sites are also possible, but they are not practically useful).

FCC has 4 octahedral sites, which means that a small interstitial atom could fit in 4 positions such that it is equally surrounded by 6 FCC lattice atoms.

These octahedral interstitial atoms can be $r = 0.414 R$ size.

FCC also has 8 tetrahedral sites, which means that a small interstitial atom could fit in 8 positions such that it is equally surrounded by 4 FCC lattice atoms.

These tetrahedral atoms can be $r = 0.225 R$ size.

Slip Systems in Face-Centered Cubic

Advanced topic, click to expand!

Slip systems are the way that atoms slide past each other when deforming. Slip systems determine many mechanical properties of materials, and is the main reason why a material will be ductile or brittle.

To understand slip system directions, you will need to be familiar with Miller Indices notation, which you can read about in this article.

The FCC close-packed planes are {111}, so those are the slip planes. Within the {111} planes, the slip direction (close-packed direction) is <110>.

By combining the 4 close-packed planes $(111), (\bar{1}11), (1\bar{1}1)$ , and $(11\bar{1})$ with 6 close-packed directions
< $110$ >, < $101$ >, < $011$ >, < $\bar{1}10$ >, < $\bar{1}01$ >, and < $0\bar{1}1$ > and dividing by two to eliminate duplicates, there are 12 independent slip systems.

12 independent slip systems is much larger than the 5 independent slip systems needed for ductility, so FCC metals are very ductile and have no ductile-to-brittle phase transition.

Final Thoughts

The Face-Centered Cubic (FCC) crystal structure is one of the most common ways that atoms can be arranged in pure solids. FCC is close-packed, which means it has the maximum APF of 0.74. Because FCC has 12 independent slip systems, it is also very ductile.

Here is a summary chart of all FCC crystal properties:

Crystal Structure	Face-centered Cubic (FCC)
Unit Cell Type	Cubic
Relationship Between Cube Edge Length a and the Atomic Radius R	a = 2R√2
Close-Packed Structure	Yes
Atomic Packing Factor (APF)	74%
Coordination Number	12
Number of Atoms per Unit Cell	4
Number of Octahedral Interstitial Sites	4
Number of Tetrahedral Interstitial Sites	8
Size of Octahedral Voids	r = 0.414 R
Size of Tetrahedral Voids	r = 0.225 R

References and Further Reading

If you want to know more about the basics of crystallography, check out this article about crystals and grains.

If you weren’t sure about the difference between crystal structure and Bravais lattice, check out this article.

I also mentioned atomic packing factor (APF) earlier in this article. This is an important concept in your introductory materials science class, so if you want a full explanation of APF, check out this page.

If you’re interested in advanced crystallography or crystallography databases, you may want to check out the AFLOW crystallographic library.

For a great reference for all crystal structures, check out “The AFLOW Library of Crystallographic Prototypes.”

Single-Element Crystal Structures and the 14 Bravais Lattices

If you want to learn about specific crystal structures, here is a list of my articles about Bravais lattices and some related crystal structures for pure elements. Face-Centered Cubic is one of these 14 Bravais lattices and also occurs as a crystal structure.

1. Simple Cubic
2. Face-Centered Cubic
2a. Diamond Cubic
3. Body-Centered Cubic
4. Simple Hexagonal
4a. Hexagonal Close-Packed
4b. Double Hexagonal Close-Packed (La-type)
5. Rhombohedral
5a. Rhombohedral Close-Packed (Sm-type)
6. Simple Tetragonal
7. Body-Centered Tetragonal
7a. Diamond Tetragonal (White Tin)
8. Simple Orthorhombic
9. Base-Centered Orthorhombic
10. Face-Centered Orthorhombic
11. Body-Centered Orthorhombic
12. Simple Monoclinic
13. Base-Centered Monoclinic
14. Triclinic

Other articles in my crystallography series include:

Introduction to Bravais Lattices
What is the Difference Between “Crystal Structure” and “Bravais Lattice”
Atomic Packing Factor
How to Read Miller Indices
How to Read Hexagonal Miller-Bravais Indices
Close-Packed Crystals and Stacking Order
Interstitial Sites
Primitive Cells
How to Read Crystallography Notation
What are Point Groups
List of Point Groups
What are Space Groups
List of Space Groups
The 7 Crystal Systems